《2025年名校课堂八年级数学上册人教版安徽专版》

7. （教材P40新增例5变式）如图，已知线段$a$，$b$和$\angle \alpha$，求作$\triangle ABC$，使得$AB = 2a$，$AC = b$，$\angle BAC=\angle \alpha$.（不写作法，保留作图痕迹）

答案： ①作一条射线$AM$；
②在射线$AM$上截取$AB = 2a$；
③作$\angle MAN=\angle\alpha$；
④在射线$AN$上截取$AC = b$；
⑤连接$BC$，则$\triangle ABC$就是所求作的三角形。
（作图痕迹需保留，即在截取线段和作角时要清晰呈现作图过程）

8. 利用尺规作$\triangle ABC$，根据下列条件作出的$\triangle ABC$不唯一的是(C)

A.$AB = 7$，$AC = 5$，$\angle A = 60^{\circ}$
B.$AC = 5$，$\angle A = 60^{\circ}$，$\angle C = 80^{\circ}$
C.$AB = 7$，$AC = 5$，$\angle B = 30^{\circ}$
D.$AB = 7$，$BC = 6$，$AC = 5$

答案： C

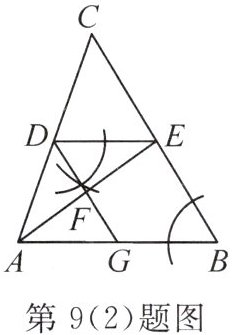
9. (1)如图，已知$\angle O = 35^{\circ}$，观察尺规作图的痕迹，可知$\angle ABC=$70°.

(2)如图，已知$DE// AB$，观察尺规作图痕迹，若$\angle CED = 60^{\circ}$，则$\angle DGA=$60°.

答案：
(1)70°
(2)60°

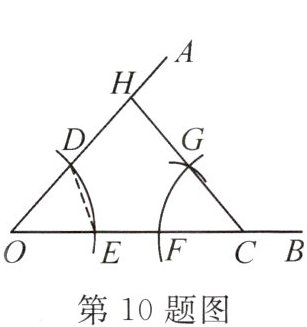
10. 如图，已知$\angle AOB=\alpha$，点$C$为射线$OB$上一点，用尺规按如下步骤作图：①以点$O$为圆心，任意长为半径作弧，交$OA$于点$D$，交$OB$于点$E$；②以点$C$为圆心，$OD$的长为半径作弧，交$OC$于点$F$；③以点$F$为圆心，$DE$的长为半径作弧，交前面的弧于点$G$；④连接$CG$并延长交$OA$于点$H$，则$\angle AHC=$2α.(用含$\alpha$的代数式表示)

答案： 2α

11. 尺规作图：
（1）如图，已知$\angle \alpha$，$\angle \beta$，且$\angle \alpha＞\angle \beta$，作$\angle DEF$，使$\angle DEF=\angle \alpha-\angle \beta$.

（2）如图，已知$\angle \alpha$和线段$a$，用尺规作一个三角形，使其一个内角等于$\angle \alpha$，另一个内角等于$2\angle \alpha$，且这两内角的夹边等于$a$.

答案： $(1)$ 作$\angle DEF = \angle\alpha-\angle\beta$
解：
1. 作$\angle AOB=\angle\alpha$：
先作射线$OA$。
以$\angle\alpha$的顶点为圆心，任意长为半径画弧，分别交$\angle\alpha$的两边于点$M$，$N$。
以$O$为圆心，同样长为半径画弧，交$OA$于点$P$。
以$P$为圆心，$MN$长为半径画弧，交前弧于点$Q$，过$Q$作射线$OB$，则$\angle AOB = \angle\alpha$。
2. 以$O$为顶点，$OB$为一边，在$\angle AOB$内部作$\angle BOC=\angle\beta$：
以$\angle\beta$的顶点为圆心，任意长为半径画弧，交$\angle\beta$的两边于$E$，$F$。
以$O$为圆心，同样长为半径画弧，交$OB$于$G$。
以$G$为圆心，$EF$长为半径画弧，交前弧于$H$，过$H$作射线$OC$，则$\angle BOC=\angle\beta$。
则$\angle AOC=\angle AOB - \angle BOC=\angle\alpha-\angle\beta$，$\angle AOC$即为所求的$\angle DEF$（可将$\angle AOC$标记为$\angle DEF$）。
$(2)$ 作三角形，使其一个内角等于$\angle\alpha$，另一个内角等于$2\angle\alpha$，且这两内角的夹边等于$a$
解：
1. 作线段$AB = a$：
用直尺画一条线段，使它的长度等于$a$，两端点分别标记为$A$，$B$。
2. 作$\angle BAC=\angle\alpha$：
以$\angle\alpha$的顶点为圆心，任意长为半径画弧，交$\angle\alpha$两边于$M$，$N$。
以$A$为圆心，同样长为半径画弧，交$AB$于$P$。
以$P$为圆心，$MN$长为半径画弧，交前弧于$Q$，过$Q$作射线$AC$，则$\angle BAC=\angle\alpha$。
3. 作$\angle ABD = 2\angle\alpha$：
先作$\angle ABE=\angle\alpha$（方法同作$\angle BAC=\angle\alpha$）。
以$BE$为一边，在$\angle ABE$外部作$\angle EBD=\angle\alpha$（同样用尺规作角的方法），则$\angle ABD = 2\angle\alpha$。
4. $AC$与$BD$相交于点$C$：
则$\triangle ABC$就是所求作的三角形。
综上，$(1)$按照上述步骤作出$\angle DEF=\angle\alpha - \angle\beta$；$(2)$按照上述步骤作出满足条件的$\triangle ABC$。

12. (1)已知：如图，线段$c$，$\angle \alpha$.求作：$\triangle ABC$，使$BC = c$，$\angle B=\angle C=\angle \alpha$.
(2)比较$\triangle ABC$中$AB$，$AC$的大小，并说明理由.
(3)猜想：在一个三角形中，相等的角所对的边相等.

答案：
(1)图略.
(2)AB=AC.理由如下:过点A作AD⊥BC于点D.
∴∠ADB=∠ADC=90°.在△ABD和△ACD中，$\left\{\begin{array}{l} ∠B=∠C,\\ ∠ADB=∠ADC,\\ AD=AD,\end{array}\right. $
∴△ABD≌△ACD(AAS).
∴AB=AC.
(3)相等