《2025年名校课堂八年级数学上册人教版安徽专版》

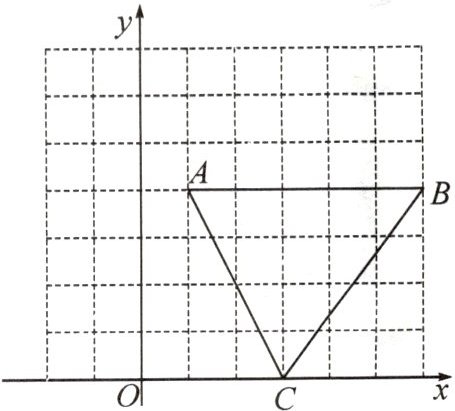
5. 如图,在 8×7 的点网格中,横、纵坐标均为整数的点叫作格点.例如:点 A(1,4),B(6,4),C(3,0)都是格点,且 BC=5.请用无刻度的直尺在给定的网格中画出下列图形,并保留作图痕迹.(画图过程用虚线表示,画图结果用实线表示)
(1)过点 A 作 AD//BC,且 AD=BC.
(2)画△ABC 的高 BE,并直接写出点 E 的坐标.
(3)在 AB 上找一点 P,使∠BCP=45°.

答案： 1. （1）
因为$BC = 5$，$AD// BC$且$AD = BC$，根据平移的性质（在网格中，水平和垂直方向的平移）。
点$B(6,4)$到$C(3,0)$，横坐标减$3$，纵坐标减$4$。那么点$A(1,4)$经过同样的平移（横坐标减$3$，纵坐标减$4$）得到$D(-2,0)$，连接$AD$，$AD$即为所求（图略）。
2. （2）
解：
设直线$AC$的解析式为$y = kx + b$，把$A(1,4)$，$C(3,0)$代入$y = kx + b$得$\begin{cases}k + b=4\\3k + b = 0\end{cases}$。
用$k + b=4$减去$3k + b = 0$：$(k + b)-(3k + b)=4 - 0$，即$k + b-3k - b = 4$，$-2k=4$，解得$k=-2$。
把$k = - 2$代入$k + b=4$，得$-2 + b=4$，$b = 6$，所以$y=-2x + 6$。
因为$BE\perp AC$，两垂直直线斜率之积为$-1$，设直线$BE$的斜率为$k_{BE}$，则$k× k_{BE}=-1$，$-2k_{BE}=-1$，$k_{BE}=\frac{1}{2}$。
又因为$B(6,4)$，设直线$BE$的解析式为$y=\frac{1}{2}x + m$，把$B(6,4)$代入得$4=\frac{1}{2}×6 + m$，$4 = 3+m$，$m = 1$，所以$y=\frac{1}{2}x + 1$。
联立$\begin{cases}y=-2x + 6\\y=\frac{1}{2}x + 1\end{cases}$，则$-2x + 6=\frac{1}{2}x + 1$。
移项得$-2x-\frac{1}{2}x=1 - 6$，$-\frac{4x}{2}-\frac{x}{2}=-5$，$-\frac{5x}{2}=-5$，解得$x = 2$。
把$x = 2$代入$y=-2x + 6$得$y=-2×2 + 6 = 2$，所以$E(2,2)$。
（也可利用网格的特点，通过构造全等三角形或面积法求$E$点坐标。$\triangle ABC$的面积$S=\frac{1}{2}× AB× h=\frac{1}{2}×5× h$，$AB = 5$（$A(1,4)$，$B(6,4)$，横坐标差为$5$，纵坐标相同），$S=\frac{1}{2}× AC× BE$，$AC=\sqrt{(1 - 3)^{2}+(4 - 0)^{2}}=\sqrt{4 + 16}=\sqrt{20}=2\sqrt{5}$，$S=\frac{1}{2}×5×4 = 10$，则$BE=\frac{2S}{AC}=\frac{2×10}{2\sqrt{5}} = 2\sqrt{5}$，再通过网格的垂直关系找到$E$点）。
3. （3）
构造等腰直角三角形：
以$C$为直角顶点，构造等腰直角三角形（利用网格）。
取格点$M(5,2)$，$N(3,2)$，连接$CM$，$CN$，$\triangle CMN$是等腰直角三角形（$CM = CN = 2$，$\angle MCN = 90^{\circ}$）。
连接$BM$，设直线$BM$与$AB$的交点为$P$。
因为$\triangle CMN$是等腰直角三角形，通过证明三角形相似或全等（$\triangle BCN$与其他三角形的关系，利用网格中的边长比例）可得$\angle BCP = 45^{\circ}$，点$P$即为所求（图略）。
综上，（2）中点$E$的坐标为$(2,2)$。

6. (2024·合肥瑶海区期末)如图,已知∠MON=70°,OB 平分∠MON,射线 OM 上有一点 A.
(1)尺规作图:作线段 OA 的垂直平分线 ED,分别交 OA,OB 于点 E,D.(不写作法,保留作图痕迹)
(2)连接 AD 并延长,交射线 ON 于点 C,则∠ACO=75.

答案： 解:
(1)图略.
(2)75

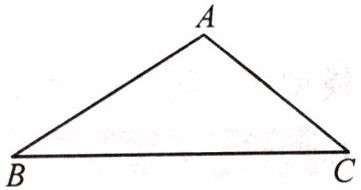
7. (2024·宿州宿城一中期末)如图,在△ABC 中,∠B=30°,∠C=40°.
(1)尺规作图:(要求:保留作图痕迹,不写作法)
①作边 AB 的垂直平分线分别交 BC,AB 于点 D,F.
②连接 AD,作∠CAD 的平分线交 BC 于点 E.
(2)在(1)所作的图中,求∠DAE 的度数.

答案： 解:
(1)图略.
(2)
∵DF 垂直平分线段 AB,
∴DB=DA.
∴∠DAB=∠B=30°.
∵∠C=40°,
∴∠BAC=180°-30°-40°=110°.
∴∠CAD=110°-30°=80°.
∵AE 平分∠DAC,
∴∠DAE=$\frac{1}{2}$∠DAC=40°.

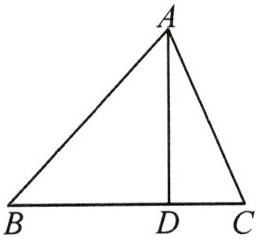
8. (2023·合肥巢湖市期末)如图,在等腰三角形 ABC 中,BA=BC,AD⊥BC 于点 D.
(1)尺规作图:过点 B 作∠ABC 的平分线交 AD 于点 E.(不写作法,保留作图痕迹)
(2)在(1)的条件下,若 AD=BD,则线段 BE,AC 之间的关系如何? 请说明理由.

答案： 解:
(1)图略.
(2)BE=AC,BE⊥AC.理由:设射线 BE 交 AC 于点 F.
∵BA=BC,
∴△ABC 为等腰三角形.
∵BF 为∠ABC 的平分线,
∴BF⊥AC.即 BE⊥AC.
∴∠BFC=90°.
∴∠CBF+∠C=90°.
∵AD⊥BC,
∴∠ADC=∠ADB=90°.
∴∠DAC+∠C=90°.
∴∠CBF=∠DAC.在△BDE 和△ADC 中,$\left\{\begin{array}{l} ∠DBE=∠DAC,\\ BD=AD,\\ ∠BDE=∠ADC,\end{array}\right. $
∴△BDE≌△ADC(ASA).
∴BE=AC.