《2025年名校课堂八年级数学上册人教版安徽专版》

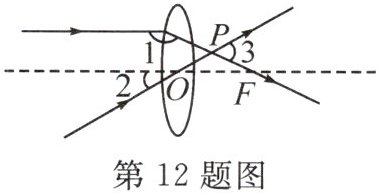
12. 新考向 跨学科(2024·芜湖期末)如图，一束平行于主光轴的光线经凸透镜折射后，其折射光线与一束经过光心$O$的光线相交于点$P$，点$F$为焦点。若$\angle 1 = 155^{\circ}$，$\angle 2 = 30^{\circ}$，则$\angle 3$的度数为(C)

A.$45^{\circ}$
B.$50^{\circ}$
C.$55^{\circ}$
D.$60^{\circ}$

答案： C

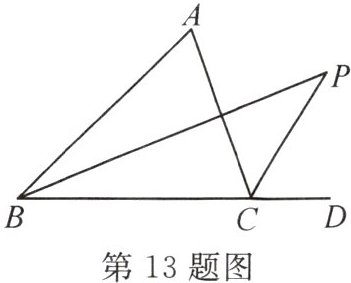
13. (2023·淮南潘集区月考)如图，在$\triangle ABC$中，$\angle ABC$的平分线与$\angle ACD$的平分线交于点$P$。若$\angle A = 60^{\circ}$，则$\angle P =$30°。

答案： 30°

14. 如图，$CE$是$\triangle ABC$的外角$\angle ACD$的平分线，$CE$交$BA$的延长线于点$E$。过点$E$作$EF // BC$，交$CA$的延长线于点$F$。
(1)若$\angle B = 36^{\circ}$，$\angle BEC = 42^{\circ}$，求$\angle F$的度数。
(2)若$\angle B = \alpha$，$\angle BEC = \beta$，则$\angle F$的度数为180°-2α-2β。(用含$\alpha$，$\beta$的式子表示)

答案： 解：
(1)
∵∠B=36°，∠BEC=42°，
∴∠ECD=∠B+∠BEC=78°.
∵CE平分∠FCD，
∴∠FCD=2∠ECD=156°.
∵EF//BC，
∴∠F=180°-∠FCD=24°.
(2)180°-2α-2β

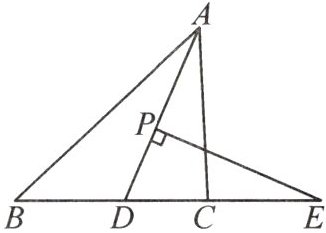
15. (2023·芜湖镜湖区期中)小明在学习中遇到这样一个问题：如图，在$\triangle ABC$中，$AD$平分$\angle BAC$，$P$为线段$AD$上的一个动点，$PE \perp AD$交$BC$的延长线于点$E$，猜想$\angle B$，$\angle ACB$，$\angle E$之间的数量关系。
(1)小明阅读题目后，没有发现数量关系与解题思路，于是尝试从具体的情况开始探索。若$\angle B = 35^{\circ}$，$\angle ACB = 85^{\circ}$，则$\angle E =$25°。
(2)小明继续探究，设$\angle B = \alpha$，$\angle ACB = \beta$($\beta ＞ \alpha$)，当点$P$在线段$AD$上运动时，求$\angle E$的度数。(用含$\alpha$，$\beta$的代数式表示)

答案： 解：
(1)25°
(2)∠E=$\frac{1}{2}(β-α)$.理由如下：
∵AD平分∠BAC，
∴∠BAD=∠CAD=$\frac{1}{2}∠BAC$.
∵∠B+∠ACB+∠BAC=180°，
∴∠BAC=180°-α-β.
∴∠BAD=$\frac{1}{2}(180°-α-β)$.
∴∠PDE=∠B+∠BAD=α+$\frac{1}{2}(180°-α-β)$=90°+$\frac{1}{2}(α-β)$.
∵PE⊥AD，
∴∠E=90°-∠PDE=90°-[90°+$\frac{1}{2}(α-β)$]=$\frac{1}{2}(β-α)$.

常用的两个基本图形公式：
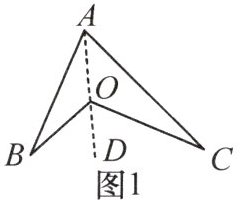
飞镖形结论：如图1，$\angle BOC = \angle BAC + \angle B + \angle C$。
推理过程：如图1，连接$AO$并延长至点$D$。
$\because \angle BOD = \angle B +$∠BAD，$\angle COD = \angle C +$∠CAD，$\therefore \angle BOC = \angle BOD + \angle COD =$∠BAC+∠B+∠C。
还可以延长$BO$交$AC$于点$E$得出此结论，试试看吧！


8字形结论：如图2，$\angle A + \angle B = \angle C + \angle D$。
推理过程：如图2，$\because \angle AOC = \angle A +$∠B，$\angle AOC = \angle C +$∠D，$\therefore \angle A +$∠B$= \angle C +$∠D。

答案： 以题明法 ∠BAD ∠CAD ∠BAC+∠B+∠C ∠B ∠D ∠B ∠D

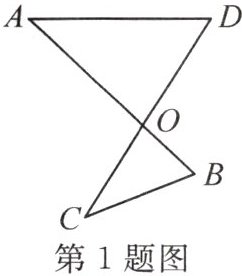
1. 如图，$AB$，$CD$相交于点$O$，连接$AD$，$BC$。若$\angle A = 43^{\circ}$，$\angle D = 57^{\circ}$，$\angle C = 37^{\circ}$，则$\angle B$的度数为63°。

答案： 63°

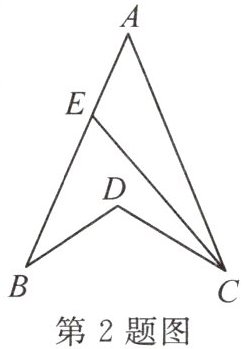
2. 如图，$CE$平分$\angle ACD$，交$AB$于点$E$。若$\angle A = 40^{\circ}$，$\angle B = 30^{\circ}$，$\angle BDC = 110^{\circ}$，则$\angle BEC$的度数为60°。

答案： 60°

3. A|人大附中校本经典题 如图，$\angle A + \angle B + \angle C + \angle D + \angle E =$__________。

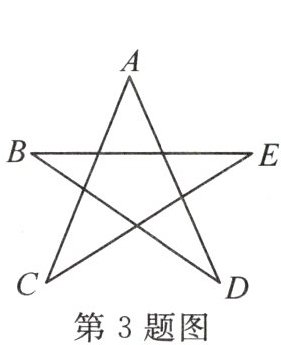
答案： 180°