第71页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
7. 命题“等边三角形的三个内角都是60°”的逆命题是
三个内角都是60°的三角形是等边三角形
,这两个命题是
(填“是”或“不是”)互逆定理.
答案:
三个内角都是60°的三角形是等边三角形 是
8. 【整体思想】(2023·亳州期末)如图,在△ABC中,AB=AC,∠A=50°,D是△ABC内的一点,连接BD,CD.若∠1=∠2,则∠D的度数为
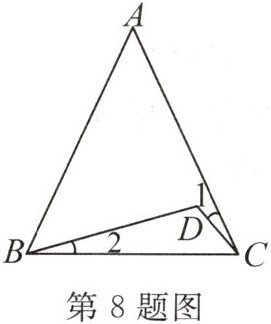
115°
.
答案:
115°
9. (2024·淮南期末)如图,在△ABC中,AC=BC=m,∠B=60°,AD是边BC上的中线.点E在边AC上,且∠EDA=30°,则直线ED与AB的位置关系是
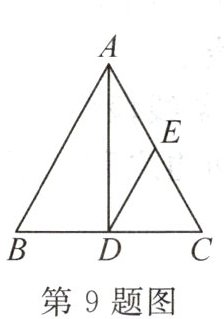
ED//AB
,ED的长为$\frac{m}{2}$
.
答案:
ED//AB $\frac{m}{2}$
10. (2024·淮南潘集区期末)如图,等腰三角形ABC的底边BC的长为8,面积是64,腰AC的垂直平分线EF分别交边AC,AB于点E,F.若D为边BC的中点,M为线段EF上一动点,则△CDM周长的最小值为
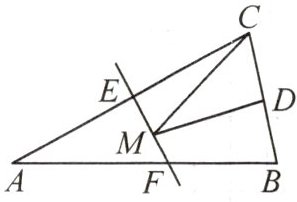
20
.
答案:
20
11. 北京四中校本经典题如图,△ABC是等边三角形,点D,E,F分别在BC,AB,CA的延长线上,且BE=AF=CD.求证:△DEF是等边三角形.
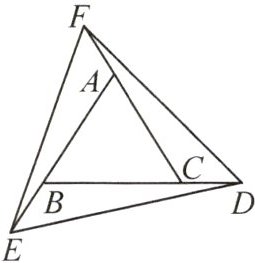

答案:
证明:
∵△ABC是等边三角形,
∴∠BAC=∠ABC=∠ACB=60°,AB=AC=BC.
∴∠EAF=∠EBD=120°.
∵BE=AF,
∴BE+AB=AF+AC,即AE=CF.
∴△AEF≌△BDE(SAS).
∴EF=ED.同理可得△AEF≌△CFD,
∴EF=FD.
∴EF=ED=FD.
∴△DEF为等边三角形.
∵△ABC是等边三角形,
∴∠BAC=∠ABC=∠ACB=60°,AB=AC=BC.
∴∠EAF=∠EBD=120°.
∵BE=AF,
∴BE+AB=AF+AC,即AE=CF.
∴△AEF≌△BDE(SAS).
∴EF=ED.同理可得△AEF≌△CFD,
∴EF=FD.
∴EF=ED=FD.
∴△DEF为等边三角形.
12. (2024·安庆潜山市期末)如图,△ABC是等边三角形,D是BC的延长线上一点,DE⊥AB于点E,EF⊥BC于点F.
(1)∠D=
(2)若CD=3AE,CF=6,则AC的长为

(1)∠D=
30°
.(2)若CD=3AE,CF=6,则AC的长为
10
.
答案:
(1)30°
(2)10
(1)30°
(2)10
13. 新考向 传统文化《蜨几图》是明朝人戈汕所作的一部组合家具的设计图(“蜨”同“蝶”),如图所示的是某蜨几设计图,其中△ABD和△CBD为“大三斜”组件(“大三斜”组件为两个全等的等腰直角三角形),已知某人位于点P处,点P与点A关于直线DQ对称,连接CP,DP.若∠ADQ=25°,则∠DCP的度数为(
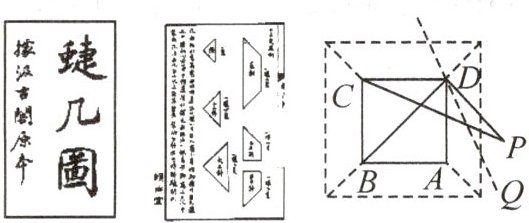
A.20°
B.21°
C.24°
D.25°
A
)
A.20°
B.21°
C.24°
D.25°
答案:
A
14. 新考向 推理能力如图,在△AB₁C₁中,AC₁=B₁C₁,∠C₁=20°,在B₁C₁上取一点C₂,延长AB₁到点B₂,使得B₁B₂=B₁C₂,在B₂C₂上取一点C₃,延长AB₂到点B₃,使得B₂B₃=B₂C₃,在B₃C₃上取一点C₄,延长AB₃到点B₄,使得B₃B₄=B₃C₄……按此操作进行下去,那么第n个三角形的内角∠ABₙCₙ=
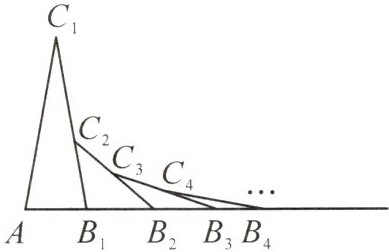
$(\frac{80}{2^{n-1}})^{\circ}$
.(用含n的式子表示)
答案:
$(\frac{80}{2^{n-1}})^{\circ}$
查看更多完整答案,请扫码查看


