《2025年点拨训练九年级数学上册人教版》

11. 用反证法证明命题“在$\triangle ABC$中,$AB\neq AC$,则$\angle B\neq \angle C$”时,首先应该假设(B)
A.$AB= AC$
B.$\angle B= \angle C$
C.$AB= AC且\angle B= \angle C$
D.$AB= AC且\angle B\neq \angle C$

答案： B

12. 用反证法证明时,假设结论“点在圆内”不成立,那么点与圆的位置关系只能是(D)
A.点在圆外
B.点在圆上
C.点在圆心上
D.点在圆上或圆外

答案： D

13. 点$O是\triangle ABC$的外心,若$\angle BOC= 80^{\circ}$,则$\angle BAC$的度数是(C)
A.$40^{\circ}$
B.$100^{\circ}$
C.$40^{\circ}或140^{\circ}$
D.$40^{\circ}或100^{\circ}$

答案： C

14. 已知$M(1,2)$,$N(3,-3)$,$P(x,y)$三点可以确定一个圆,则以下$P$点坐标不满足要求的是(C)
A.$(3,5)$
B.$(-3,5)$
C.$(-1,7)$
D.$(1,-2)$

答案： C

15. 如图,$O为等腰三角形ABC$的外心,$AB= AC$,连接$OB$,记$\angle C= \alpha$,$\angle CBO= \beta$,则$\alpha$,$\beta$满足的关系式为(D)
A.$2\beta-\alpha=90^{\circ}$
B.$2\beta-\alpha=180^{\circ}$
C.$\frac{1}{2}\beta+\alpha=90^{\circ}$
D.$2\alpha-\beta=90^{\circ}$

答案： D

16. [2024广州中考]如图,$\odot O$中,弦$AB的长为4\sqrt{3}$,点$C在\odot O$上,$OC\perp AB$,$\angle ABC= 30^{\circ}$。$\odot O所在的平面内有一点P$,若$OP= 5$,则点$P与\odot O$的位置关系是(C)
A.点$P在\odot O$上
B.点$P在\odot O$内
C.点$P在\odot O$外
D.无法确定

答案： 1. 首先，根据垂径定理：
因为$OC\perp AB$，$AB = 4\sqrt{3}$，由垂径定理$AC = BC$，$AB = 2AD$（设$OC$与$AB$交于点$D$），所以$AD=\frac{1}{2}AB = 2\sqrt{3}$。
又因为$\angle ABC = 30^{\circ}$，在$Rt\triangle ABD$中，$\angle ADB = 90^{\circ}$，根据圆周角定理$\angle AOC = 2\angle ABC$（同弧所对的圆心角是圆周角的$2$倍），所以$\angle AOC=60^{\circ}$。
2. 然后，在$Rt\triangle AOD$中：
已知$\angle AOD = 60^{\circ}$，$\angle OAD = 30^{\circ}$，设$OD = x$，则$OA = 2x$。
根据勾股定理$OA^{2}=OD^{2}+AD^{2}$，即$(2x)^{2}=x^{2}+(2\sqrt{3})^{2}$。
展开式子得$4x^{2}=x^{2}+12$。
移项得$4x^{2}-x^{2}=12$，即$3x^{2}=12$，解得$x = 2$（$x\gt0$）。
所以$OA=2x = 4$，即$\odot O$的半径$r = 4$。
3. 最后，判断点$P$与$\odot O$的位置关系：
已知$OP = 5$，因为$d=OP = 5$，$r = 4$，且$d\gt r$。
根据点与圆的位置关系：设圆的半径为$r$，点到圆心的距离为$d$，当$d\gt r$时，点在圆外。所以点$P$在$\odot O$外，答案是C。

17. 如图,要把残破的圆片复原完整。已知弧上的三点$A$,$B$,$C$。
(1)用尺规作图法找出$\overset{\frown}{BC}所在圆的圆心O$。(保留作图痕迹,不写作法)
(2)若$\triangle ABC$是等腰三角形,底边$BC= 8cm$,腰$AB= 5cm$,求圆片的半径$R$。

答案：
解：
(1)如图,点O即为所求.
　　　　　　
(2)如图,连接AO,BO,AO交BC于点E.
∵AB=AC,
∴$\overset{\frown}{AB}$=$\overset{\frown}{AC}$.
∴OA⊥BC.
∴BE= $\frac{1}{2}$BC=4 cm.在Rt△ABE中,AE= $\sqrt{AB^{2}-BE^{2}}$= $\sqrt{5^{2}-4^{2}}$=3(cm).在Rt△BEO中,OB²=BE²+OE²,即R²=4²+(R-3)²,解得R= $\frac{25}{6}$.
∴圆片的半径R为 $\frac{25}{6}$cm.

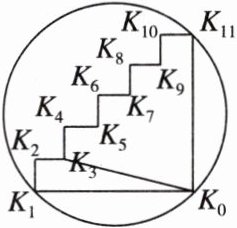
18. 如图,一个直角锯齿卡尺(所有角均为直角),$K_0$,$K_1$,$K_{11}$都在圆上,且$K_0K_1= K_0K_{11}= 5$。卡尺所有锯齿高度和水平宽度都为$1$,如：$K_1K_2= K_2K_3= 1$。
(1)圆心在卡尺内部还是外部？请说明理由。
(2)过点$K_0$,$K_1$,$K_{11}$的圆的半径是多少？
(3)连接$K_0K_3$,以点$K_0$为圆心,$K_0K_3$为半径画圆,直接写出点$K_7$,$K_9与\odot K_0$的位置关系。

答案： 解：
(1)圆心在卡尺内部,理由如下：连接K₁K₁₁,
∵K₀,K₁,K₁₁都在圆上,易知∠K₁K₀K₁₁=90°,
∴K₁K₁₁为圆的直径,
∴圆心在Rt△K₁K₀K₁₁的斜边K₁K₁₁的中点处,
∴圆心在卡尺内部.
(2)
∵K₀K₁=K₀K₁₁=5,∠K₁K₀K₁₁=90°,
∴K₁K₁₁= $\sqrt{5^{2}+5^{2}}$=5$\sqrt{2}$.
∵K₁K₁₁是过点K₀,K₁,K₁₁的圆的直径,
∴过点K₀,K₁,K₁₁的圆的半径是 $\frac{1}{2}$K₁K₁₁= $\frac{5\sqrt{2}}{2}$.
(3)K₇在⊙K₀内部,K₉在⊙K₀上.