第56页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
1. 某商场降价销售一批名牌衬衫,已知所获利润 $ y $ (元) 与降价 $ x $ (元) 之间的关系式是 $ y = - 2 x ^ { 2 } + 60 x + 800 $,则获得的利润最大为(
A.15 元
B.400 元
C.800 元
D.1 250 元
D
)A.15 元
B.400 元
C.800 元
D.1 250 元
答案:
D
2. [教材 $ P _ { 51 } $ 习题 $ T _ { 2 } $ 变式] 某种商品每件进价为 20 元,调查发现:在某段时间内若以每件 $ x $ 元 ($ 20 \leq x \leq 30 $,且 $ x $ 为整数) 出售,可卖出 $ ( 30 - x ) $ 件,要使利润最大,每件的售价应为(
A.24 元
B.25 元
C.28 元
D.30 元
B
)A.24 元
B.25 元
C.28 元
D.30 元
答案:
B
3. [2025 广州越秀区月考] 端午节前夕,某商店购入一批进价为 8 元/袋的粽子,销售过程中发现:日销量 $ y $ (袋) 与售价 $ x $ (元/袋) 满足如图所示的一次函数关系.
(1) 求 $ y $ 与 $ x $ 之间的函数解析式;
(2) 当每袋粽子的售价定为多少元时,日销售利润最大?最大日销售利润是多少元?
]
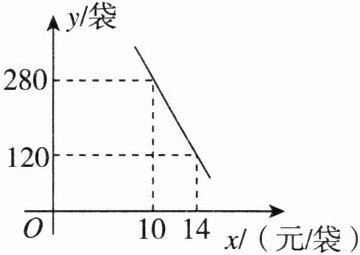
(1) 求 $ y $ 与 $ x $ 之间的函数解析式;
(2) 当每袋粽子的售价定为多少元时,日销售利润最大?最大日销售利润是多少元?
]

答案:
解:
(1)设 y 与 x 之间的函数解析式为 y=kx+b,将(10,280),(14,120)代入,得{280=10k+b,120=14k+b,解得{k=-40,b=680,
∴y 与 x 之间的函数解析式为 y=-40x+680.
(2)设日销售利润为 w 元,由题意得 w=(x-8)y=(x-8)(-40x+680)=-40x²+1000x-5440=-40(x-12.5)²+810,
∵-40<0,
∴当 x=12.5 时,w 有最大值,最大值为 810,
∴当每袋粽子的售价定为 12.5 元时,日销售利润最大,最大日销售利润是 810 元.
(1)设 y 与 x 之间的函数解析式为 y=kx+b,将(10,280),(14,120)代入,得{280=10k+b,120=14k+b,解得{k=-40,b=680,
∴y 与 x 之间的函数解析式为 y=-40x+680.
(2)设日销售利润为 w 元,由题意得 w=(x-8)y=(x-8)(-40x+680)=-40x²+1000x-5440=-40(x-12.5)²+810,
∵-40<0,
∴当 x=12.5 时,w 有最大值,最大值为 810,
∴当每袋粽子的售价定为 12.5 元时,日销售利润最大,最大日销售利润是 810 元.
4. 当进价为 80 元/件的某衬衣定价为 100 元/件时,每月可卖出 2 000 件,售价每上涨 1 元,月销售量便减少 5 件,那么每月售出衬衣的总件数 $ y $ (件) 与衬衣售价 $ x $ (元/件) 之间的函数关系式为
y=-5x+2500
,每月利润 $ W $ (元) 与衬衣售价 $ x $ (元/件) 之间的函数关系式为W=-5x²+2900x-200000
.
答案:
y=-5x+2500;W=-5x²+2900x-200000
5. 情境题 安全意识 一人一盔安全守规,一人一带平安常在!某商店销售一批头盔,售价为每顶 80 元,每月可售出 200 顶. 在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价 1 元,每月可多售出 20 顶. 已知头盔的进价为每顶 50 元,则该商店每月获得最大利润时,每顶头盔的售价为(
A.60 元
B.65 元
C.70 元
D.75 元
C
)A.60 元
B.65 元
C.70 元
D.75 元
答案:
C
6. [2024 烟台中考节选] 每年 5 月的第三个星期日为全国助残日,今年的主题是“科技助残,共享美好生活”. 康宁公司新研发了一批便携式轮椅计划在该月销售. 根据市场调查,每辆轮椅盈利 200 元时,每天可售出 60 辆;单价每降低 10 元,每天可多售出 4 辆. 公司决定在成本不变的情况下降价销售,但每辆轮椅的利润不低于 180 元,设每辆轮椅降价 $ x $ 元,每天的销售利润为 $ y $ 元.
(1) 求 $ y $ 与 $ x $ 之间的函数关系式;
(2) 每辆轮椅降价多少元时,每天的销售利润最大?最大利润为多少元?
(1) 求 $ y $ 与 $ x $ 之间的函数关系式;
(2) 每辆轮椅降价多少元时,每天的销售利润最大?最大利润为多少元?
答案:
解:
(1)由题意,得 y=(200-x)(60+x/10×4)=-2/5x²+20x+12000.
(2)
∵每辆轮椅的利润不低于 180 元,
∴200-x≥180,解得 x≤20.
∵y=-2/5x²+20x+12000=-2/5(x-25)²+12250,
∴当 x<25 时,y 随 x 的增大而增大,
∴当 x=20 时,y 取得最大值,最大值为-2/5×(20-25)²+12250=12240.答:每辆轮椅降价 20 元时,每天的销售利润最大,最大利润为 12240 元.
(1)由题意,得 y=(200-x)(60+x/10×4)=-2/5x²+20x+12000.
(2)
∵每辆轮椅的利润不低于 180 元,
∴200-x≥180,解得 x≤20.
∵y=-2/5x²+20x+12000=-2/5(x-25)²+12250,
∴当 x<25 时,y 随 x 的增大而增大,
∴当 x=20 时,y 取得最大值,最大值为-2/5×(20-25)²+12250=12240.答:每辆轮椅降价 20 元时,每天的销售利润最大,最大利润为 12240 元.
查看更多完整答案,请扫码查看


