《2025年点拨训练九年级数学上册人教版》

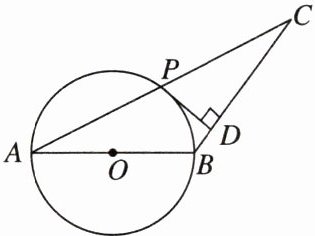
5. 新考向 传统文化 独轮车俗称“手推车”,又名鹿车等,西汉时已在一些田间隘道上出现。北宋时正式出现独轮车名称,在北方,独轮车几乎与毛驴起着同样的运输作用。如图是从独轮车中抽象出来的几何模型。在$\triangle ABC$中,$AB = BC$,以$\triangle ABC的边AB为直径作\odot O$,交$AC于点P$,且$PD \perp BC$,垂足为$D$。求证：$PD是\odot O$的切线。

答案： 证明：连接OP，
∵AB=BC，
∴∠A=∠C.
∵OA=OP，
∴∠OPA=∠A，
∴∠OPA=∠C，
∴OP//BC.
∵PD⊥BC，
∴PD⊥OP.
又
∵OP是⊙O的半径，
∴PD是⊙O的切线.

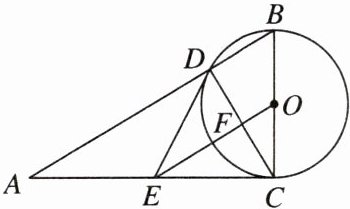
6. 如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,以$BC为直径的\odot O交AB于点D$,$E是AC$的中点,$OE交CD于点F$。判断直线$DE与\odot O$的位置关系,并说明理由。

答案： 解：直线DE与⊙O相切.
理由如下：连接OD.
∵E是AC的中点，
∴AE=EC.
又
∵OB=OC，
∴OE是△ABC的中位线.
∴OE//AB.
∵BC是⊙O的直径，
∴∠BDC=90°.
∴∠OFC=∠BDC=90°，即OE⊥CD.
又
∵OD=OC，
∴∠DOE=∠COE.
在△EOD和△EOC中，
$\left\{\begin{array}{l}OD=OC,\\ ∠DOE=∠COE,\\ OE=OE,\end{array}\right.$
∴△EOD≌△EOC.
∴∠EDO=∠ECO=90°，即OD⊥DE.
又
∵OD是⊙O的半径，
∴直线DE与⊙O相切.)

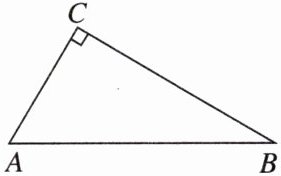
7. [2024广东中考]如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$。
(1)实践与操作：用尺规作图法作$\angle A的平分线AD交BC于点D$；(保留作图痕迹,不要求写作法)
(2)应用与证明：在(1)的条件下,以点$D$为圆心,$DC长为半径作\odot D$。求证：$AB与\odot D$相切。

答案：

(1)解：如图①，AD即为所求作.

(2)证明：如图②，作DE⊥AB于点E，
∵AD是的平分线，DC⊥AC，DE⊥AB，
∴DE=DC.
∴DE是⊙D的半径，
∴AB与⊙D相切.

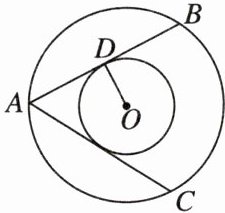
8. 如图,在两个同心圆中,$AB$,$AC$都是大圆的弦,且$AB = AC$,$AB与小圆相切于点D$,则$AC$与小圆相切吗？请说明理由。

答案：
解：AC与小圆相切.
理由如下：过点O作OE⊥AC于点E，连接OA，如图.

由切线的性质可知OD⊥AB，
由垂径定理可知AD=DB，AE=EC.
∵AB=AC，
∴AD=AE.
在Rt△AEO和Rt△ADO中，
$\left\{\begin{array}{l}AO=AO,\\ AE=AD,\end{array}\right.$
∴Rt△AEO≌Rt△ADO(HL)，
∴OE=OD，
∴OE为小圆的半径，
∴AC与小圆相切.