第118页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
17. 新考向传统文化[2024河北中考]扇文化是中华优秀传统文化的组成部分,在我国有着深厚的底蕴.如图,某折扇张开的角度为120°时,扇面面积为S,该折扇张开的角度为n°时,扇面面积为$S_{n}$,若$m= \frac{S_{n}}{S}$,则m与n关系的图象大致是( )
]

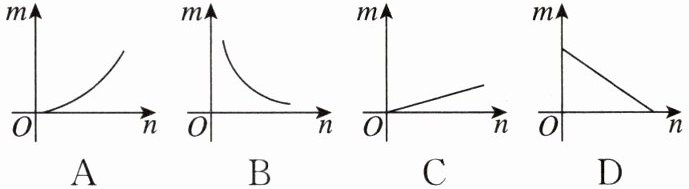
C
]


答案:
C
18. 某校九年级学生参加社会实践,学习编织圆锥形工艺品.若这种圆锥的母线长为40厘米,底面圆的半径为30厘米,则该圆锥的侧面积为(
A.700π平方厘米
B.900π平方厘米
C.1200π平方厘米
D.1600π平方厘米
C
)A.700π平方厘米
B.900π平方厘米
C.1200π平方厘米
D.1600π平方厘米
答案:
C
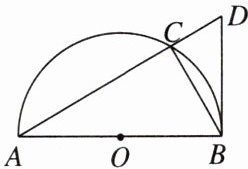
19. [2024江西中考]如图,AB是半圆O的直径,点D是弦AC延长线上一点,连接BD,BC,∠D= ∠ABC= 60°.
(1)求证:BD是半圆O的切线;
(2)当BC= 3时,求$\overset{\frown}{AC}$的长.
]
(1)求证:BD是半圆O的切线;
(2)当BC= 3时,求$\overset{\frown}{AC}$的长.
]

答案:
(1)证明:
∵AB 是半圆 O 的直径,
∴∠ACB=90°.
∵∠D=∠ABC=60°,
∴∠CAB=90°-∠ABC=30°,
∴∠ABD=180°-∠CAB-∠D=90°,即 BD⊥OB,
又
∵OB 是半圆 O 的半径,
∴BD 是半圆 O 的切线.
(2)解:连接 OC,
∵OC=OB,∠CBA=60°,
∴△OCB 为等边三角形,
∴∠COB=60°,OC=CB=3,
∴∠AOC=180°-∠COB=120°,
∴$\widehat{AC}$的长为$\frac{120}{180}×\pi×3$=2π.
(1)证明:
∵AB 是半圆 O 的直径,
∴∠ACB=90°.
∵∠D=∠ABC=60°,
∴∠CAB=90°-∠ABC=30°,
∴∠ABD=180°-∠CAB-∠D=90°,即 BD⊥OB,
又
∵OB 是半圆 O 的半径,
∴BD 是半圆 O 的切线.
(2)解:连接 OC,
∵OC=OB,∠CBA=60°,
∴△OCB 为等边三角形,
∴∠COB=60°,OC=CB=3,
∴∠AOC=180°-∠COB=120°,
∴$\widehat{AC}$的长为$\frac{120}{180}×\pi×3$=2π.
20. 已知△ABC的边BC的长为$4\sqrt{2}$cm,且△ABC内接于半径为4cm的⊙O,求∠A的度数.
答案:
解:分两种情况:
①当∠A 是锐角时,连接 OB,OC,过点 O 作 OD⊥BC 于点 D,如图所示,则∠ODB=90°,
又
∵OB=OC,
∴BD=$\frac{1}{2}$BC=2$\sqrt{2}$cm,∠BOD=$\frac{1}{2}$∠BOC.
在 Rt△BOD 中,OB=4cm,OB²=OD²+BD²,
∴4²=OD²+(2$\sqrt{2}$)²,
∴OD=2$\sqrt{2}$cm(负值已舍去).
∴BD=OD.
∴∠BOD=45°.
∴∠BOC=90°.
∴∠A=$\frac{1}{2}$∠BOC=45°;
②当∠A 是钝角时,易知∠A=180°-45°=135°.
综上所述,∠A 的度数为 45°或 135°.
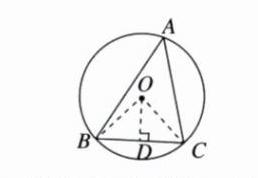
解:分两种情况:
①当∠A 是锐角时,连接 OB,OC,过点 O 作 OD⊥BC 于点 D,如图所示,则∠ODB=90°,
又
∵OB=OC,
∴BD=$\frac{1}{2}$BC=2$\sqrt{2}$cm,∠BOD=$\frac{1}{2}$∠BOC.
在 Rt△BOD 中,OB=4cm,OB²=OD²+BD²,
∴4²=OD²+(2$\sqrt{2}$)²,
∴OD=2$\sqrt{2}$cm(负值已舍去).
∴BD=OD.
∴∠BOD=45°.
∴∠BOC=90°.
∴∠A=$\frac{1}{2}$∠BOC=45°;
②当∠A 是钝角时,易知∠A=180°-45°=135°.
综上所述,∠A 的度数为 45°或 135°.

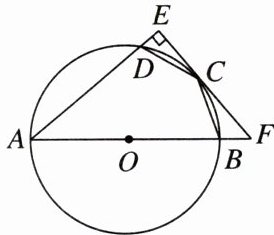
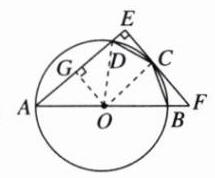
21. 如图,四边形ABCD内接于⊙O,AB为⊙O的直径,过点C作CE⊥AD,交AD的延长线于点E,延长EC,AB交于点F,∠ECD= ∠BCF.
(1)求证:CE为⊙O的切线;
(2)若DE= 1,CD= 3,求⊙O的半径.
]
(1)求证:CE为⊙O的切线;
(2)若DE= 1,CD= 3,求⊙O的半径.
]

答案:
(1)证明:如图,连接 OC.
∵OB=OC,
∴∠OCB=∠OBC.
∵四边形 ABCD 内接于$\odot O$,
∴易得∠CDE=∠OBC.
∴∠CDE=∠OCB.
∵CE⊥AD,
∴∠CDE+∠ECD=90°.
又
∵∠ECD=∠BCF,
∴∠OCB+∠BCF=90°,
即∠OCF=90°,
∴OC⊥EF.
∵OC 是$\odot O$的半径,
∴CE 为$\odot O$的切线.
(2)解:如图,过点 O 作 OG⊥AE 于点 G,连接 OD,则∠OGE=90°.
又
∵CE⊥AE,OC⊥EF,
∴易得四边形 OGEC 是矩形.
∴OC=EG,OG=EC.
设$\odot O$的半径为 x,则 EG=OC=OD=x,
∵DE=1,
∴GD=x - 1.
在 Rt△CDE 中,CD=3,
∴EC=$\sqrt{3^2-1^2}$=2$\sqrt{2}$.
∴OG=2$\sqrt{2}$.
在 Rt△OGD 中,由勾股定理得 OD²=OG²+DG²,即 x²=(2$\sqrt{2}$)²+(x - 1)²,解得 x=4.5.
∴$\odot O$的半径是 4.5.

(1)证明:如图,连接 OC.
∵OB=OC,
∴∠OCB=∠OBC.
∵四边形 ABCD 内接于$\odot O$,
∴易得∠CDE=∠OBC.
∴∠CDE=∠OCB.
∵CE⊥AD,
∴∠CDE+∠ECD=90°.
又
∵∠ECD=∠BCF,
∴∠OCB+∠BCF=90°,
即∠OCF=90°,
∴OC⊥EF.
∵OC 是$\odot O$的半径,
∴CE 为$\odot O$的切线.
(2)解:如图,过点 O 作 OG⊥AE 于点 G,连接 OD,则∠OGE=90°.
又
∵CE⊥AE,OC⊥EF,
∴易得四边形 OGEC 是矩形.
∴OC=EG,OG=EC.
设$\odot O$的半径为 x,则 EG=OC=OD=x,
∵DE=1,
∴GD=x - 1.
在 Rt△CDE 中,CD=3,
∴EC=$\sqrt{3^2-1^2}$=2$\sqrt{2}$.
∴OG=2$\sqrt{2}$.
在 Rt△OGD 中,由勾股定理得 OD²=OG²+DG²,即 x²=(2$\sqrt{2}$)²+(x - 1)²,解得 x=4.5.
∴$\odot O$的半径是 4.5.
查看更多完整答案,请扫码查看


