第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
1. [教材$P_{52}习题T_{4}$变式]已知一个直角三角形两直角边之和为20 cm,则这个直角三角形的最大面积为 (
A.$25cm^{2}$
B.$50cm^{2}$
C.$100cm^{2}$
D.不确定
B
)A.$25cm^{2}$
B.$50cm^{2}$
C.$100cm^{2}$
D.不确定
答案:
B
2. 如图是一个长为20 m,宽为16 m的矩形花园,根据需要将它的长缩短x m,宽增加x m,要使修改后的花园面积达到最大,则x的值为 (
A.1
B.1.5
C.2
D.4
C
)A.1
B.1.5
C.2
D.4
答案:
C
3. [教材$P_{49}$探究1变式][2024泰安中考改编]如图,小明的父亲想用长为60 m的栅栏,再借助房屋的外墙围成一个矩形的菜园,已知房屋外墙长40 m,则可围成的菜园的最大面积是 (
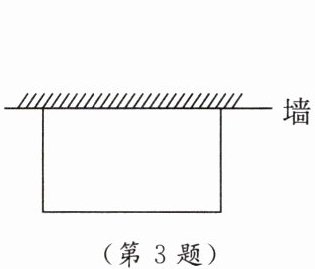
A.$420m^{2}$
B.$450m^{2}$
C.$480m^{2}$
D.$500m^{2}$
B
)
A.$420m^{2}$
B.$450m^{2}$
C.$480m^{2}$
D.$500m^{2}$
答案:
B
4. [2025杭州模拟]如图,在长为20 m、宽为14 m的矩形花圃里建有等宽的十字形小路,若小路的宽不超过1 m,则花圃中阴影部分的面积 (
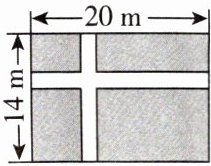
A.有最小值$247m^{2}$
B.有最小值$266m^{2}$
C.有最大值$247m^{2}$
D.有最大值$266m^{2}$
A
)
A.有最小值$247m^{2}$
B.有最小值$266m^{2}$
C.有最大值$247m^{2}$
D.有最大值$266m^{2}$
答案:
A
5. [教材$P_{52}习题T_{5}$变式]如图,小轩同学想做一个菱形风筝,现在有一根长120 cm的竹竿,他准备把它截成两段做成风筝的龙骨(即菱形的对角线AC,BD),请你帮他设计一下,当AC=
60
cm时,菱形的面积最大,最大为1800
$cm^{2}$.
答案:
60;1 800
6. 新视角 动点探究题如图,在矩形ABCD中,AB= 6 cm,BC= 12 cm,点P从点A出发,沿AB边向点B以1 cm/s的速度运动,点Q从点B出发,沿BC边向点C以2 cm/s的速度运动,且P,Q两点同时出发,分别到达B,C两点后就停止运动.
(1)设运动开始后第t s,五边形APQCD的面积为$Scm^{2}$,写出S关于t的函数解析式,并指出自变量t的取值范围;
(2)在(1)的条件下,t为何值时,S有最小值?最小值是多少?
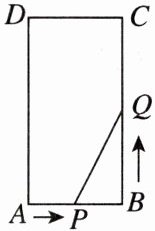
(1)设运动开始后第t s,五边形APQCD的面积为$Scm^{2}$,写出S关于t的函数解析式,并指出自变量t的取值范围;
(2)在(1)的条件下,t为何值时,S有最小值?最小值是多少?

答案:
解:
(1)第t s时,AP=t cm,BQ=2t cm,故PB=(6-t)cm,
∴S△PBQ=$\frac{1}{2}$×(6-t)×2t=(-t²+6t)cm².
∴S=6×12-(-t²+6t)=t²-6t+72 (0<t<6).
(2)
∵S=t²-6t+72=(t-3)²+63,
∴当t=3时,S有最小值,最小值是63.
(1)第t s时,AP=t cm,BQ=2t cm,故PB=(6-t)cm,
∴S△PBQ=$\frac{1}{2}$×(6-t)×2t=(-t²+6t)cm².
∴S=6×12-(-t²+6t)=t²-6t+72 (0<t<6).
(2)
∵S=t²-6t+72=(t-3)²+63,
∴当t=3时,S有最小值,最小值是63.
查看更多完整答案,请扫码查看


