《2025年点拨训练九年级数学上册人教版》

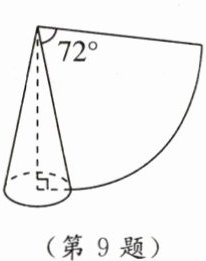
9. [2024广州中考]如图,圆锥的侧面展开图是一个圆心角为$72^{\circ}$的扇形,若扇形的半径$l$是5,则该圆锥的体积是(D)

A.$\frac{3\sqrt{11}}{8}\pi$
B.$\frac{\sqrt{11}}{8}\pi$
C.$2\sqrt{6}\pi$
D.$\frac{2\sqrt{6}}{3}\pi$

答案： D

10. 如图,在矩形纸片$ABCD$中,$AD= 6cm$,把它分割成正方形纸片$ABFE和矩形纸片EFCD$后,分别裁出扇形$BAF$和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则$AB$的长为(B)
A.3.5cm
B.4cm
C.4.5cm
D.5cm

答案： B

11. 如图,小珍同学用半径为10cm、圆心角为$100^{\circ}$的扇形纸片,制作一个底面半径为2.5cm的圆锥侧面,则圆锥上粘贴部分的面积是$\frac{25\pi}{9}$$cm^{2}$.

答案： $\frac{25\pi}{9}$

12. 如图所示的漏斗,圆锥形内壁的母线$OB$长为6cm,开口直径为6cm.
(1)因直管部分堵塞,漏斗内灌满了水,则水深为$3\sqrt{3}$cm；(结果保留根号)
(2)若将贴在内壁的滤纸(忽略漏斗管口处和滤纸接缝处)展开,则展开滤纸的圆心角的度数为180°.

答案：
(1)$3\sqrt{3}$　
(2)180°

13. 【问题情境】工人在制作圆锥形物品时,通常要先确定扇形的圆心角度数,再度量裁剪材料.如图①,将一个底面半径为$r$的圆锥侧面展开,可得到一个半径为$l$,圆心角为$n^{\circ}$的扇形.
(1)【探索尝试】图①中,圆锥底面周长与其侧面展开图的弧长______(填“相等”或“不相等”),若$r= 3$,$l= 9$,则$n= $______；
(2)【解决问题】为操作简便,工人希望能简洁求$n$的值,请用含$r$,$l的式子表示n$；
(3)【拓展延伸】图②是一种圆锥形纸质生日帽,$AB= 6cm$,$l= 6cm$,点$C是PB$的中点,现要从点$A到点C再到点A$之间拉一条装饰彩带,求彩带长度的最小值.

(1)相等；120
(2)$n=$$\frac{360r}{l}$
(3)$6\sqrt{5}$cm

答案： 解:
(1)相等;120
(2)由圆锥的底面周长等于其侧面展开图的弧长，
　得$2\pi r=\frac{n\pi l}{180}$，
∴n=$\frac{2\pi r×180}{\pi l}=\frac{360r}{l}$.
(3)
∵l=6cm,r=$\frac{1}{2}AB$ = 3cm,
∴n=$\frac{360×3}{6}$ = 180,
∴圆锥的侧面展开后得到的扇形的圆心角度数为180°,如图，设展开后点A,C的对应点分别是点A',C'，连接A'C,A'P,A'C',易知彩带长度的最小值为A'C+A'C' = 2A'C,∠A'PC=$\frac{1}{2}×180^{\circ}$ = 90°.
∵PA'=PB = 6cm,点C是PB的中点，
∴PC=$\frac{1}{2}PB$ = 3cm,
∴在Rt△A'PC中,
A'C=$\sqrt{PA'^{2}+PC^{2}}$ = $\sqrt{6^{2}+3^{2}}$ = $3\sqrt{5}$(cm),
∴彩带长度的最小值为2A'C = $6\sqrt{5}$cm.