第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
14. 易错题若关于x的一元二次方程$(m-3)x^{2}+m^{2}x= 9x+5$化为一般形式后不含一次项,则m的值为(
A.0
B.±3
C.3
D.-3
D
)A.0
B.±3
C.3
D.-3
答案:
D
15. 若关于x的一元二次方程$ax^{2}-bx-20= 0满足a+b= 20$,则方程必有一根为(
A.-1
B.1
C.±1
D.无法确定
A
)A.-1
B.1
C.±1
D.无法确定
答案:
A
16. 新考向 数学文化《九章算术》中有一题:“今有二人同所立,甲行率七,乙行率三,乙东行,甲南行十而斜东北与乙会.问甲、乙行各几何?”大意是说:“如图,甲、乙二人同时从同一地点出发,甲的速度为7,乙的速度为3.乙一直向东走,甲先向南走10,后又向北偏东方向走了一段后与乙相遇,那么相遇时,甲、乙各走了多少?”设甲、乙二人从出发到相遇的时间为x,根据题意,下列方程正确的是(
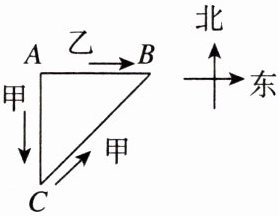
A.$(3x)^{2}+(7x)^{2}= 10^{2}$
B.$(3x)^{2}+10^{2}= (7x)^{2}$
C.$(3x)^{2}+10^{2}= (7x-10)^{2}$
D.$(3x+10)^{2}+10^{2}= (7x)^{2}$
C
)
A.$(3x)^{2}+(7x)^{2}= 10^{2}$
B.$(3x)^{2}+10^{2}= (7x)^{2}$
C.$(3x)^{2}+10^{2}= (7x-10)^{2}$
D.$(3x+10)^{2}+10^{2}= (7x)^{2}$
答案:
C
17. (1)[2024南充中考]已知m是方程$x^{2}+4x-1= 0$的一个根,则$(m+5)(m-1)$的值为
(2)已知a是方程$x^{2}+2025x-1= 0$的一个根,则代数式$a(a+1)(a-1)+2025a^{2}+1$的值是
-4
.(2)已知a是方程$x^{2}+2025x-1= 0$的一个根,则代数式$a(a+1)(a-1)+2025a^{2}+1$的值是
1
.
答案:
(1)-4
(2)1
(1)-4
(2)1
18. 根据下列问题列一元二次方程,并将所列方程化成一般形式:
(1)某班之间为相互鼓励,每两人之间进行一次击掌,共击掌595次.求本班有多少名同学;
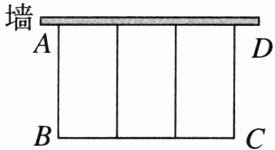
(2)如图,用100m长的围栏围成总面积为$400m^{2}$的三个大小相同的矩形羊圈,羊圈的一面靠墙(墙足够长),求AB的长.
]
(1)某班之间为相互鼓励,每两人之间进行一次击掌,共击掌595次.求本班有多少名同学;
(2)如图,用100m长的围栏围成总面积为$400m^{2}$的三个大小相同的矩形羊圈,羊圈的一面靠墙(墙足够长),求AB的长.
]

答案:
解:
(1)设本班有 x 名同学,依题意,得$\frac{1}{2}x(x-1)=595$,化成一般形式为 x²-x-1190=0.
(2)设 AB 的长为 x m,由题意,得x(100-4x)=400,化成一般形式为x²-25x+100=0.
(1)设本班有 x 名同学,依题意,得$\frac{1}{2}x(x-1)=595$,化成一般形式为 x²-x-1190=0.
(2)设 AB 的长为 x m,由题意,得x(100-4x)=400,化成一般形式为x²-25x+100=0.
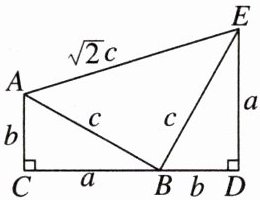
19. 新视角 新定义题如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是$Rt△ABC和Rt△BED$的三边长,易知$AE= \sqrt {2}c$,这时我们把关于x的形如$ax^{2}+\sqrt {2}cx+b= 0$的一元二次方程称为“勾系一元二次方程”,比如$3x^{2}+5\sqrt {2}x+4= 0$是“勾系一元二次方程”.请解决下列问题:
(1)方程$x^{2}+2x+1= 0$____“勾系一元二次方程”(填“是”或“不是”);
(2)若$x= -1$是“勾系一元二次方程”$ax^{2}+\sqrt {2}cx+b= 0$的一个根,且四边形ACDE的周长是12,求$△ABC$的面积.
(1)
(2)
(1)方程$x^{2}+2x+1= 0$____“勾系一元二次方程”(填“是”或“不是”);
(2)若$x= -1$是“勾系一元二次方程”$ax^{2}+\sqrt {2}cx+b= 0$的一个根,且四边形ACDE的周长是12,求$△ABC$的面积.

(1)
是
(2)
2
答案:
解:
(1)是
(2)把 x=-1 代入方程,得$a-\sqrt{2}c+b=0$,即$a+b=\sqrt{2}c$.
由题意得$2a+2b+\sqrt{2}c=12$,即$2(a+b)+\sqrt{2}c=12$,$\therefore 3\sqrt{2}c=12$.$\therefore c=2\sqrt{2}$.
$\therefore a+b=\sqrt{2}c=4$.易知$a²+b²=c²=8$,$(a+b)²=a²+2ab+b²=16$,$\therefore ab=4$.$\therefore S_{\triangle ABC}=\frac{1}{2}ab=2$.
(1)是
(2)把 x=-1 代入方程,得$a-\sqrt{2}c+b=0$,即$a+b=\sqrt{2}c$.
由题意得$2a+2b+\sqrt{2}c=12$,即$2(a+b)+\sqrt{2}c=12$,$\therefore 3\sqrt{2}c=12$.$\therefore c=2\sqrt{2}$.
$\therefore a+b=\sqrt{2}c=4$.易知$a²+b²=c²=8$,$(a+b)²=a²+2ab+b²=16$,$\therefore ab=4$.$\therefore S_{\triangle ABC}=\frac{1}{2}ab=2$.
查看更多完整答案,请扫码查看


