第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
1. 下列选项中,属于旋转的是(
A.电梯升降的过程
B.火箭升空的过程
C.雨滴下落的过程
D.转盘转动的过程
D
)A.电梯升降的过程
B.火箭升空的过程
C.雨滴下落的过程
D.转盘转动的过程
答案:
D
2. [2025廊坊期中]如图,教室内的地面上有个倒地的簸箕,手柄CB与箕面AB垂直,手柄CB与水平地面的夹角$∠BCA= 31^{\circ }$,小明将它扶起(将簸箕绕点A顺时针旋转)后平放在地面上,则箕面AB绕点A旋转的度数为(
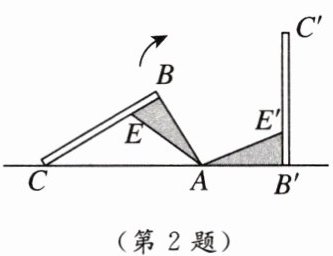
A.$59^{\circ }$
B.$119^{\circ }$
C.$120^{\circ }$
D.$121^{\circ }$
D
)
A.$59^{\circ }$
B.$119^{\circ }$
C.$120^{\circ }$
D.$121^{\circ }$
答案:
D
3. [2024无锡中考]如图,在$△ABC$中,$∠B= 80^{\circ }$,$∠C= 65^{\circ }$,将$△ABC$绕点A逆时针旋转得到$△AB'C'$.当$AB'$落在AC上时,$∠BAC'$的度数为(
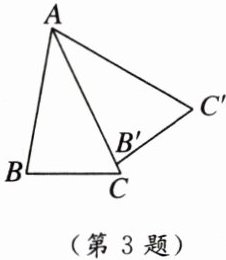
A.$65^{\circ }$
B.$70^{\circ }$
C.$80^{\circ }$
D.$85^{\circ }$
B
)
A.$65^{\circ }$
B.$70^{\circ }$
C.$80^{\circ }$
D.$85^{\circ }$
答案:
B
4. 如图,在正方形网格中,$△EFG绕某一点旋转某一角度得到△RPQ$,则旋转中心是(
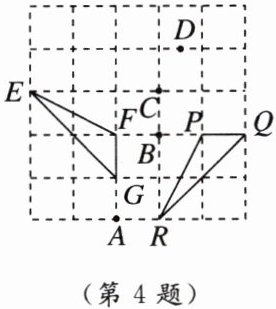
A.点A
B.点B
C.点C
D.点D
C
)
A.点A
B.点B
C.点C
D.点D
答案:
C
5. [2024湖北中考]如图,点A的坐标是$(-4,6)$,将线段OA绕点O顺时针旋转$90^{\circ }$,点A的对应点的坐标是(
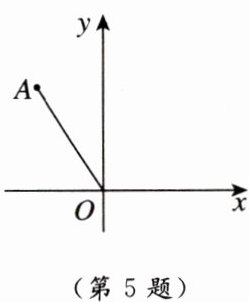
A.$(4,6)$
B.$(6,4)$
C.$(-6,-4)$
D.$(-4,-6)$
B
)
A.$(4,6)$
B.$(6,4)$
C.$(-6,-4)$
D.$(-4,-6)$
答案:
B
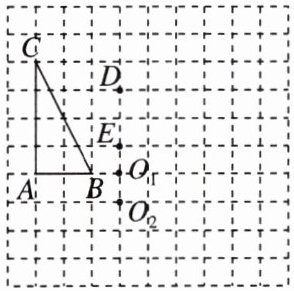
6. 如图,网格中每个小正方形的边长均为1,$△ABC绕着一点按顺时针方向旋转得到△DEF$,D,E,F分别为点A,B,C的对应点,三角形的顶点均在格点(网格线的交点)上.
(1)$BC= $____,旋转中心为点____(填“$O_{1}$”或“$O_{2}$”),旋转角度为____$^{\circ }$;
(2)在图中补全$△DEF$.
(1)$BC= $____,旋转中心为点____(填“$O_{1}$”或“$O_{2}$”),旋转角度为____$^{\circ }$;
(2)在图中补全$△DEF$.

答案:
解:
(1)$2\sqrt{5}$;$O_{1}$;90
(2)如图.
解:
(1)$2\sqrt{5}$;$O_{1}$;90
(2)如图.

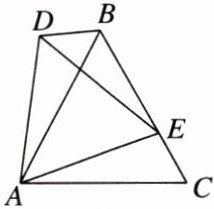
7. [2025武汉期中]如图,在$△ABC$中,$AB= AC$,点E是BC边上任意一点,将$△AEC$绕点A逆时针旋转得到$△ADB$,点E的对应点为点D,连接DE.
(1)求证:$∠ABC= ∠ABD$;
(2)若$BD// AC$,求$∠AED$的度数.
(1)求证:$∠ABC= ∠ABD$;
(2)若$BD// AC$,求$∠AED$的度数.

答案:
(1)证明:$\because AB=AC$,$\therefore \angle ABC=\angle ACB$.
$\because$将$\triangle AEC$绕点A逆时针旋转得到$\triangle ADB$,$\therefore \angle ACB=\angle ABD$,$\therefore \angle ABC=\angle ABD$.
(2)解:$\because BD// AC$,$\therefore \angle ABD=\angle BAC$.
$\because \angle ABC=\angle ABD$,$\angle ABC=\angle ACB$,$\therefore \angle BAC=\angle ACB=\angle ABC$,$\therefore \angle BAC=\angle ACB=\angle ABC=60^{\circ}$.
$\because$将$\triangle AEC$绕点A逆时针旋转得到$\triangle ADB$,$\therefore \angle EAC=\angle DAB$,$AE=AD$,$\therefore \angle EAC+\angle BAE=\angle DAB+\angle BAE$,即$\angle DAE=\angle BAC$,$\therefore \angle DAE=60^{\circ}$.$\therefore \triangle ADE$是等边三角形,$\therefore \angle AED=60^{\circ}$.
(1)证明:$\because AB=AC$,$\therefore \angle ABC=\angle ACB$.
$\because$将$\triangle AEC$绕点A逆时针旋转得到$\triangle ADB$,$\therefore \angle ACB=\angle ABD$,$\therefore \angle ABC=\angle ABD$.
(2)解:$\because BD// AC$,$\therefore \angle ABD=\angle BAC$.
$\because \angle ABC=\angle ABD$,$\angle ABC=\angle ACB$,$\therefore \angle BAC=\angle ACB=\angle ABC$,$\therefore \angle BAC=\angle ACB=\angle ABC=60^{\circ}$.
$\because$将$\triangle AEC$绕点A逆时针旋转得到$\triangle ADB$,$\therefore \angle EAC=\angle DAB$,$AE=AD$,$\therefore \angle EAC+\angle BAE=\angle DAB+\angle BAE$,即$\angle DAE=\angle BAC$,$\therefore \angle DAE=60^{\circ}$.$\therefore \triangle ADE$是等边三角形,$\therefore \angle AED=60^{\circ}$.
查看更多完整答案,请扫码查看


