《2025年新教材新评估九年级数学全一册北师大版》

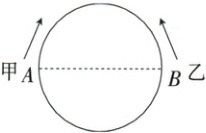
6. 某校为培育青少年科技创新能力,举办了动漫制作活动。小明设计了点做圆周运动的一个雏形,如图所示,甲、乙两点分别从直径的两端点 $A$,$B$ 沿顺时针、逆时针的方向同时做圆周运动,甲的路程 $l(cm)$ 与运动时间 $t(s)$ 满足关系 $l = t^{2}+3t(t\geq0)$,乙以 8 cm/s 的速度匀速运动,半圆的长度为 42 cm。
(1) 甲运动 4 s 后的路程是多少？
(2) 甲、乙从开始运动到第一次相遇时,它们运动了多长时间？

答案： 解:
(1)当$t = 4\ s$时,$l = t^{2} + 3t = 16 + 12 = 28(cm)$.答:甲运动4 s后的路程是28 cm.
(2)由题图可知,甲、乙第一次相遇时,它们的路程和为半圆长42 cm,甲的路程为$(t^{2} + 3t)cm$,乙的路程为$8t\ cm$,则$t^{2} + 3t + 8t = 42$.解得$t = 3$或$t = -14$(不合题意,舍去).答:甲、乙从开始运动到第一次相遇时,它们运动了3 s.

7. 如图,在矩形 $ABCD$ 中,$AB = 16\ cm$,$AD = 6\ cm$。动点 $P$,$Q$ 分别从点 $A$,$C$ 同时出发,点 $P$ 以 3 cm/s 的速度向点 $B$ 运动,点 $Q$ 以 2 cm/s 的速度向点 $D$ 运动,点 $P$ 到达点 $B$ 时停止运动,点 $Q$ 也随之停止。问：
(1) $P$,$Q$ 两点从出发开始几秒后,四边形 $PB-CQ$ 的面积为 33 $cm^{2}$？
(2) 几秒后点 $P$、点 $Q$ 间的距离是 10 cm？
(3) $P$,$Q$ 两点间的距离何时最小？

答案： 解:
(1)当运动时间为$t\ s$时,$PB = (16 - 3t)cm$,$CQ = 2t\ cm$.依题意,得$\frac{1}{2}×(16 - 3t + 2t)×6 = 33$,解得$t = 5$.答:$P,Q$两点从出发开始5 s后,四边形$PBCQ$的面积为$33\ cm^{2}$.
(2)设出发后$x\ s$$P,Q$两点间的距离是10 cm.则$AP = 3x\ cm$,$CQ = 2x\ cm$.作$QM\perp AB$于点$M$,则$PM = |16 - 2x - 3x| = |16 - 5x|$,$(16 - 5x)^{2} + 6^{2} = 10^{2}$.解得$x = \frac{8}{5} = 1.6$或$x = \frac{24}{5} = 4.8$.$\therefore$点$P,Q$出发后1.6 s或4.8 s,$P,Q$间的距离是10 cm.
(3)$\because PQ = \sqrt{(16 - 5x)^{2} + 6^{2}}$,$\therefore$当$16 - 5x = 0$,即$P,Q$两点出发$\frac{16}{5}\ s$时,$PQ$最小.