《2025年新教材新评估九年级数学全一册北师大版》

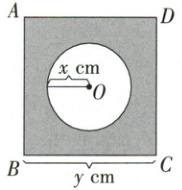
9. 如图,正方形 $ ABCD $ 和 $ \odot O $ 的周长之和为 $ 20cm $,设圆的半径为 $ xcm $,正方形的边长为 $ ycm $,阴影部分的面积为 $ Scm^{2} $。当 $ x $ 在一定范围内变化时,$ y $ 和 $ S $ 都随 $ x $ 的变化而变化,则 $ y $ 与 $ x $,$ S $ 与 $ x $ 满足的函数关系分别是(B)

A.一次函数关系、一次函数关系
B.一次函数关系、二次函数关系
C.二次函数关系、二次函数关系
D.二次函数关系、一次函数关系

答案： B

10. 某商品的进价为每件 $ 30 $ 元,现在的售价为每件 $ 40 $ 元,每星期可卖出 $ 150 $ 件。市场调查发现：如果每件的售价每涨 $ 1 $ 元(每件售价不能高于 $ 45 $ 元),那么每星期少卖出 $ 10 $ 件。设每件涨价 $ x $($ x $ 为非负整数)元,每星期的销量为 $ y $ 件。
(1) 求 $ y $ 与 $ x $ 之间的函数关系式及自变量 $ x $ 的取值范围；
(2) 设每星期的利润为 $ W $ 元,写出 $ W $ 与 $ x $ 之间的函数关系式,并判断 $ W $ 是不是 $ x $ 的二次函数。

答案： 解:
(1)由题意,得每星期的销量y=150-10x=-10x+150(0≤x≤5且x为整数).
(2)由题意,得W=(x+40-30)(150-10x)=-10x²+50x+1500(0≤x≤5且x为整数). W是x的二次函数.

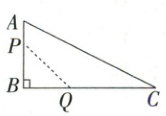
11. 如图,在 $ \triangle ABC $ 中,$ \angle B = 90^{\circ} $,$ AB = 12m $,$ BC = 24m $,动点 $ P $ 从点 $ A $ 开始沿边 $ AB $ 向点 $ B $ 以 $ 2m/s $ 的速度运动(不与点 $ B $ 重合),动点 $ Q $ 从点 $ B $ 开始沿边 $ BC $ 向点 $ C $ 以 $ 4m/s $ 的速度运动(不与点 $ C $ 重合)。如果 $ P,Q $ 两点同时出发,设运动时间为 $ xs $,四边形 $ APQC $ 的面积为 $ ym^{2} $。
(1) 求 $ y $ 与 $ x $ 之间的函数关系式。
(2) 求自变量 $ x $ 的取值范围。
(3) 四边形 $ APQC $ 的面积能否等于 $ 172m^{2} $？若能,求出运动的时间；若不能,请说明理由。

答案： 解:
(1)y=4x²-24x+144.
(2)自变量x的取值范围为0＜x＜6.
(3)不能. 理由:令4x²-24x+144=172, 解得x₁=7,x₂=-1(不合题意,舍去). 因为0＜x＜6,所以x=7不在范围内. 所以四边形APQC的面积不能等于172m².