《2025年新教材新评估九年级数学全一册北师大版》

6. 某综合性文化休闲公园种了数万株观赏树木,园内桥、廊、亭、榭多不胜数。如图,相关部门计划在公园内的长 $32m$、宽 $20m$ 的近似矩形湖面上修筑宽度固定的观景长廊(图中阴影部分),要使湖面剩余部分(空白部分)的面积为 $540m^{2}$,则长廊的宽应为2 $m$。

答案： 2

7. 《田亩比类乘除捷法》中记载了一道题：“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步？”译文：一个矩形的面积为 $864$ 平方步,宽比长少 $12$ 步,宽和长各多少步？设矩形的宽为 $x$ 步,由题意,可列方程$x(x+12)=864$。

答案： $x(x+12)=864$

8. 如图①,窗帘的褶皱是按照窗户的实际宽度将窗帘布料以一定比例加宽做成的,褶皱之后的窗帘显得更飘逸、灵动。其中,窗宽度的 $1.5$ 倍为平褶皱,窗宽度的 $2$ 倍为波浪褶皱。如图②,小莉房间的窗户呈长方形,窗户的宽度 $(AD)$ 比高度 $(AB)$ 少 $0.5m$,某种窗帘的价格为 $120$ 元$/m^{2}$。如果以波浪褶皱的方式制作该种窗帘的费用比以平褶皱的方式制作的费用多 $180$ 元,求小莉房间窗户的宽度与高度。

答案： 解:设小莉房间窗户的宽度为x m,则高度为$(x+0.5)m.$
根据题意,得$(2-1.5)\cdot x\cdot (x+0.5)×120=180.$
解得$x_{1}=-2$(舍去),$x_{2}=1.5.$
$\therefore x=1.5,x+0.5=2.$
答:小莉房间窗户的宽度为1.5 m,高度为2 m.

9. 为全面落实劳动教育,某校在如图所示的两面成直角的围墙角落(墙足够长),用总长为 $28m$ 的篱笆围成了一个长方形苗圃 $OABC$。设 $AB = x m,BC = y m$。
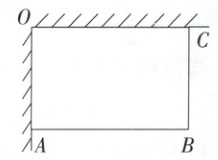
(1) 求苗圃 $OABC$ 的面积(用含 $x$ 的代数式表示)；
(2) 若苗圃 $OABC$ 的面积为 $192m^{2}$,现要在苗圃 $OABC$ 的对角线上修一条小道 $AC$,求小道 $AC$ 的长。

答案：
(1)依题意有$y=28-x.$
∴苗圃OABC的面积为$AB\cdot BC=xy=x(28-x)=-x^{2}+28x.$
(2)由
(1)可得$192=-x^{2}+28x,$
$\therefore x^{2}-28x+192=0.$
解得$x_{1}=16,x_{2}=12.$
当$x=16$时,$y=12;$
当$x=12$时,$y=16.$
∵四边形OABC是长方形,$\therefore ∠ABC=90^{\circ }.$
连接AC,
$\therefore AC=\sqrt {x^{2}+y^{2}}=\sqrt {12^{2}+16^{2}}=20(m).$