《2025年新教材新评估九年级数学全一册北师大版》

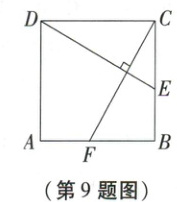
9. 如图,在边长为 4√3 的正方形 ABCD 中,∠CDE = 30°,DE ⊥ CF,则 AF 的长为4√3 - 4.[img]

答案： 4√3 - 4

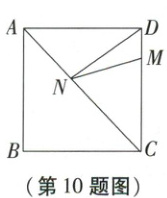
10. 如图,正方形 ABCD 的边长为 8,点 M 在 DC 上且 DM = 2,N 是 AC 上的一动点,则 DN + MN 的最小值是10.[img]

答案： 10

11. 如图,在正方形 ABCD 中,对角线 AC,BD 相交于点 O,点 E,F 是对角线 AC 上的两点,且 AE = CF,连接 DE,DF,BE,BF. 若 AB = 4,AE = √2,求四边形 BEDF 的周长.[img]

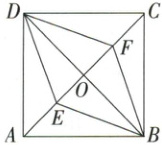
答案： 解：
∵AB=AD=4，
∴BD=√(AB²+AD²)=4√2.
由正方形对角线相等且互相垂直平分可得：
AC=BD=4√2，DO=BO=2√2=OA=OC.
又AE=CF=√2，
∴OE=OF=2√2 - √2=√2.
∴四边形BEDF为平行四边形.
∵∠DOE=90°，
∴四边形BEDF是菱形.
∴DE=√(DO²+EO²)=√((2√2)²+(√2)²)=√10.
∴4DE=4√10.
故四边形BEDF的周长为4√10.

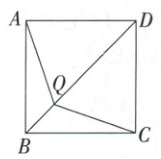
12. 如图,在正方形 ABCD 中,Q 为对角线 BD 上一点(DQ ＞ BQ),连接 AQ,CQ.
(1) 求证：AQ = CQ.
(2) 过点 Q 作 QR ⊥ BD 交 BC 于点 R,延长 CB 至点 H,使 BH = CR,连接 AH.
① 依题意补全图形；
② 用等式表示 AH 与 CQ 之间的数量关系,并证明.[img]

答案：

(1)证明：
∵四边形ABCD是正方形，
∴AB=BC，∠ABQ=∠CBQ=45°.
又BQ=BQ，
∴△ABQ≌△CBQ(SAS).
∴AQ=CQ.
(2)解：①补全图形，如图.

②AH=√2CQ.
证明：如图，连接HQ.
∵QR⊥BD，∠QBR=45°，
∴∠QRB=45°.
∴∠QBR=∠QRB.
∴BQ=RQ，∠QBH=∠QRC=135°.
又
∵HB=CR，
∴△QBH≌△QRC(SAS).
∴QH=QC，∠HQB=∠RQC.
由
(1)可知△ABQ≌△CBQ，
∴∠AQB=∠BQC.
∴∠AQH+∠HQB=∠BQR+∠RQC.
∴∠AQH=∠BQR=90°.
∵AQ=QC，
∴AQ=HQ.
∴△AQH是等腰直角三角形.
∴AH=√2AQ.
∴AH=√2CQ.