第98页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
【例】如图,在边长为2的正方形ABCD中,以点B为圆心、AB为半径构造扇形ABC,点P是弧$\overset{\frown}{AC}$上一动点,过点P作EF⊥BC,分别交AD,BC于点E,F.记AE,PE,$\overset{\frown}{AP}构成的封闭区域为S_{1}$,PF,FC,$\overset{\frown}{PC}构成的封闭区域为S_{2}$,当$S_{1}与S_{2}$面积相等时,BF的长为(

A.1
B.$\frac{4}{3}$
C.$\sqrt{2}$
D.$\frac{\pi}{2}$
解析:设封闭区域ABFP面积为S,
$\therefore S_{1}= AB\cdot BF-S= 2BF-S$,$S_{2}= S_{扇形BAC}-S= \frac{90×\pi×2^{2}}{360}-S= \pi-S$.
$\because S_{1}= S_{2}$,$\therefore 2BF-S= \pi-S$,$\therefore BF= \frac{\pi}{2}$.
答案:D
D
).
A.1
B.$\frac{4}{3}$
C.$\sqrt{2}$
D.$\frac{\pi}{2}$
解析:设封闭区域ABFP面积为S,
$\therefore S_{1}= AB\cdot BF-S= 2BF-S$,$S_{2}= S_{扇形BAC}-S= \frac{90×\pi×2^{2}}{360}-S= \pi-S$.
$\because S_{1}= S_{2}$,$\therefore 2BF-S= \pi-S$,$\therefore BF= \frac{\pi}{2}$.
答案:D
答案:
解:设封闭区域ABFP的面积为S。
因为四边形ABCD是边长为2的正方形,EF⊥BC,
所以AB=BC=2,四边形ABFE是矩形,AE=BF,EF=AB=2。
$S_{1}$为AE,PE,$\overset{\frown}{AP}$构成的封闭区域,其面积等于矩形ABFE的面积减去封闭区域ABFP的面积,即$S_{1}=AB\cdot BF - S = 2BF - S$。
扇形BAC的半径为AB=2,圆心角为90°,其面积为$\frac{90\pi×2^{2}}{360}=\pi$。
$S_{2}$为PF,FC,$\overset{\frown}{PC}$构成的封闭区域,其面积等于扇形BAC的面积减去封闭区域ABFP的面积,即$S_{2}=\pi - S$。
因为$S_{1}=S_{2}$,所以$2BF - S = \pi - S$,解得$BF=\frac{\pi}{2}$。
答案:D
因为四边形ABCD是边长为2的正方形,EF⊥BC,
所以AB=BC=2,四边形ABFE是矩形,AE=BF,EF=AB=2。
$S_{1}$为AE,PE,$\overset{\frown}{AP}$构成的封闭区域,其面积等于矩形ABFE的面积减去封闭区域ABFP的面积,即$S_{1}=AB\cdot BF - S = 2BF - S$。
扇形BAC的半径为AB=2,圆心角为90°,其面积为$\frac{90\pi×2^{2}}{360}=\pi$。
$S_{2}$为PF,FC,$\overset{\frown}{PC}$构成的封闭区域,其面积等于扇形BAC的面积减去封闭区域ABFP的面积,即$S_{2}=\pi - S$。
因为$S_{1}=S_{2}$,所以$2BF - S = \pi - S$,解得$BF=\frac{\pi}{2}$。
答案:D
1.(第十六届全国初中数学竞赛)有两个同心圆,大圆周上有4个不同的点,小圆周上有2个不同的点,则这6个点可以确定的不同直线最少有(
A.6条
B.8条
C.10条
D.12条
B
).A.6条
B.8条
C.10条
D.12条
答案:
B
2.(第八届"学用杯"全国数学知识应用竞赛初赛)在一场赈灾演出中,根据需要必须用灯光照亮舞台中一个半径为2米的圆形区域,但由于当地条件简陋,当时没有这样的灯,舞台监督要求用另一种可照半径为1米的灯代替,那么至少需这样的代用灯( ).
A.5盏
B.6盏
C.7盏
D.8盏
A.5盏
B.6盏
C.7盏
D.8盏
答案:
C [解析] 如图,设半径为2的圆的圆心是O,在圆周上作正六边形ABCDEF,其边长都是2.再分别以各边中点为圆心作六个半径为1的圆,加上中间的一个半径为1的圆,共需7盏灯.故选C.

C [解析] 如图,设半径为2的圆的圆心是O,在圆周上作正六边形ABCDEF,其边长都是2.再分别以各边中点为圆心作六个半径为1的圆,加上中间的一个半径为1的圆,共需7盏灯.故选C.

3.(江苏初中数学竞赛第1试)如图,O为圆心,若已知圆心角∠AOC= $x^{\circ}$,则∠CBD为(
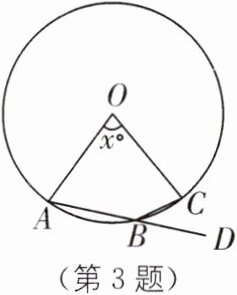
A.$180^{\circ}-x^{\circ}$
B.$90^{\circ}-x^{\circ}$
C.$\frac{1}{2}x^{\circ}$
D.$90^{\circ}-\frac{1}{2}x^{\circ}$
C
).
A.$180^{\circ}-x^{\circ}$
B.$90^{\circ}-x^{\circ}$
C.$\frac{1}{2}x^{\circ}$
D.$90^{\circ}-\frac{1}{2}x^{\circ}$
答案:
C
4.(江苏初中数学竞赛第1试)如图,在平面直角坐标系中,ABCDEFGH是正八边形,点A的坐标为(2,0),点B的坐标为(0,2),则点E的坐标为______
$(2+2\sqrt{2},4+2\sqrt{2})$
.
答案:
$(2+2\sqrt{2},4+2\sqrt{2})$
5.平面上有100个点$P_{1},P_{2},P_{3},…,P_{99},P_{100}$.试说明,可以画一个圆,使得圆内恰有k个点,另外100-k(1≤k<100)个点均在该圆外部.
答案:
过$P_{1},P_{2},\cdots,P_{100}$中每两点都作它们的垂直平分线,这样画出的垂直平分线有有限条.在平面上任取一点O不在上述所画的直线上.根据中垂线的性质知$OP_{1},OP_{2},\cdots,OP_{100}$两两不等,不妨从小到大排序,设$OP_{1}<OP_{2}<OP_{3}<\cdots<OP_{99}<OP_{100}$,取$r=\frac{OP_{k}+OP_{k+1}}{2}$,则$OP_{1}<OP_{2}<OP_{3}<\cdots<OP_{k}<r$,故$P_{1},P_{2},\cdots,P_{k}$都在$\odot O$内.而$r<OP_{k+1}<\cdots<OP_{100}$,故$P_{k+1},P_{k+2},\cdots,P_{99},P_{100}$这$(100 - k)$个点均在半径为r的$\odot O$外.按照上述方法就可以作出符合要求的圆.
6.以O为圆心、1为半径的圆内有一定点A,过A引互相垂直的弦PQ,RS.求PQ+RS的最大值和最小值.
答案:
如图,设$OA = a$(定值),过点O作$OB\perp PQ,OC\perp RS$,B,C为垂足.设$OB = x,OC = y(0\leqslant x\leqslant a,0\leqslant y\leqslant a)$,且$x^{2}+y^{2}=a^{2}$.

$\therefore PQ = 2PB = 2\sqrt{1 - x^{2}}$,$RS = 2\sqrt{1 - y^{2}}$,$\therefore PQ + RS = 2(\sqrt{1 - x^{2}}+\sqrt{1 - y^{2}})$,$\therefore (PQ + RS)^{2}=4(2 - a^{2}+2\sqrt{1 - a^{2}+x^{2}y^{2}})$,而$x^{2}y^{2}=x^{2}(a^{2}-x^{2})=-(x^{2}-\frac{a^{2}}{2})^{2}+\frac{a^{4}}{4}$.当$x^{2}=\frac{a^{2}}{2}$时,$(x^{2}y^{2})_{最大值}=\frac{a^{4}}{4}$.此时$(PQ + RS)_{最大值}=\sqrt{4(2 - a^{2}+2 - a^{2})}=2\sqrt{4 - 2a^{2}}$.当$x^{2}=0$或$x^{2}=a^{2}$时,$(x^{2}y^{2})_{最小值}=0$,此时$(PQ + RS)_{最小值}=2(1+\sqrt{1 - a^{2}})$.
如图,设$OA = a$(定值),过点O作$OB\perp PQ,OC\perp RS$,B,C为垂足.设$OB = x,OC = y(0\leqslant x\leqslant a,0\leqslant y\leqslant a)$,且$x^{2}+y^{2}=a^{2}$.

$\therefore PQ = 2PB = 2\sqrt{1 - x^{2}}$,$RS = 2\sqrt{1 - y^{2}}$,$\therefore PQ + RS = 2(\sqrt{1 - x^{2}}+\sqrt{1 - y^{2}})$,$\therefore (PQ + RS)^{2}=4(2 - a^{2}+2\sqrt{1 - a^{2}+x^{2}y^{2}})$,而$x^{2}y^{2}=x^{2}(a^{2}-x^{2})=-(x^{2}-\frac{a^{2}}{2})^{2}+\frac{a^{4}}{4}$.当$x^{2}=\frac{a^{2}}{2}$时,$(x^{2}y^{2})_{最大值}=\frac{a^{4}}{4}$.此时$(PQ + RS)_{最大值}=\sqrt{4(2 - a^{2}+2 - a^{2})}=2\sqrt{4 - 2a^{2}}$.当$x^{2}=0$或$x^{2}=a^{2}$时,$(x^{2}y^{2})_{最小值}=0$,此时$(PQ + RS)_{最小值}=2(1+\sqrt{1 - a^{2}})$.
查看更多完整答案,请扫码查看


