《2025年实验班提优训练九年级数学上册浙教版》

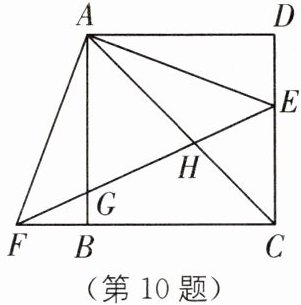
10. (2025·杭州萧山区期末)如图,E 是正方形 ABCD 的边 CD 上一点,连结 AE,将△ADE 顺时针旋转 90°得到△ABF,连结 EF,分别交 AB,AC 于点 G,H. 若△AFG 与△AEC 相似,则 $\frac{AG}{BG}$= ______.

答案：
10.2+2$\sqrt{2}$　[解析]如图，延长FE交AD的延长线于点T，过点E作EJ⊥AC于点J.
　　　　　　
∵四边形ABCD是正方形，
∴∠ADE=∠BAD=90°，∠ACD=∠DAC=45°，AD=CD.由旋转变换的性质可知∠BAF=∠DAE，DE=BF.
∵△AFG与△AEC相似，
∴∠BAF=∠EAC，
∴∠DAE=∠EAC.
∵ED⊥AD，EJ⊥AC，
∴ED=EJ.角平分线上的点到角两端的距离相等.
∵EC=$\sqrt{2}$EJ，
∴EC=$\sqrt{2}$DE.设DE=BF=m，则EC=$\sqrt{2}$m，AD=CD=(1+$\sqrt{2}$)m.
∵∠DAC=45°，
∴∠DAE=∠EAC=22.5°，
∴∠AED=67.5°.
∵∠DAE=∠BAF，
∴∠EAF=∠DAB=90°.
∵AE=AF，
∴∠AEF=45°，
∴∠DET=180° - 45° - 67.5°=67.5°，
∴∠T=∠DAE=22.5°，
∴EA=ET.
∵ED⊥AT，
∴AD=DT=(1+$\sqrt{2}$)m.
∵BF//AT，
∴$\frac{AG}{GB}=\frac{AT}{BF}=\frac{2(1+\sqrt{2})m}{m}=2+2\sqrt{2}$.

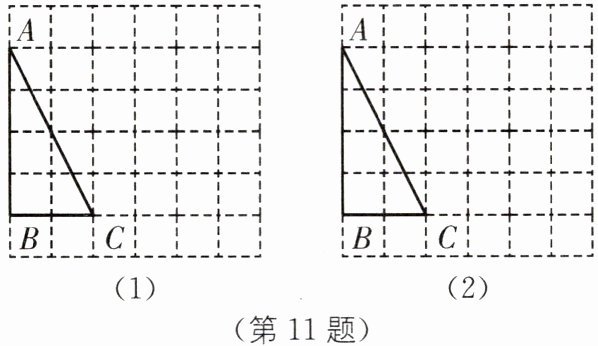
11. (2024·宁波北仑区期末)在 6×6 的方格纸中,请按下列要求画出格点三角形(顶点均在格点上).
(1)在图(1)中将△ABC 绕点 C 顺时针旋转 90°,画出旋转后得到的△A'B'C；
(2)在图(2)中画出一个与△ABC 相似的△ACD,且使得相似比不为 1.(画出一个即可)

答案：
11.
(1)如图
(1)，△A'B'C'即为所求；
(2)如图
(2)，△ACD即为所求(答案不唯一).
　　　

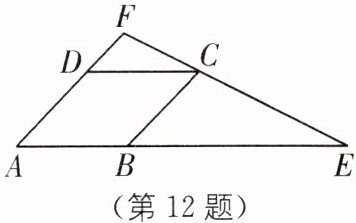
12. 如图,已知菱形 ABCD 的边长为 4,延长 AB 到点 E,使 EB= 2AB,连结 EC 并延长交 AD 的延长线于点 F,如果△EBC∽△EAF,试求 AF 的长.

答案： 12.
∵菱形ABCD的边长为4，
∴AB=BC=4，
∴EB=2AB=8，
∴EA=EB+AB=12.
∵△EBC∽△EAF，
∴$\frac{BC}{AF}=\frac{EB}{EA}$，
∴$\frac{4}{AF}=\frac{8}{12}$，
∴AF=6.
归纳总结　本题考查的是相似三角形的性质，掌握相似三角形的对应角相等、对应边成比例是解题的关键.

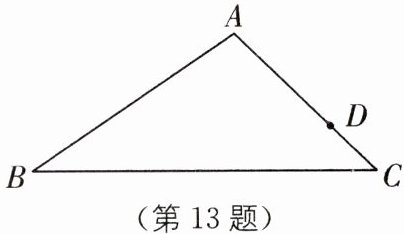
13. 分类讨论思想 中考新考法 满足条件的结论开放 如图,在△ABC 中,AB= 4 cm,AC= 3 cm,BC= 6 cm,D 是 AC 上一点,AD= 2 cm,点 P 从 C 出发沿 C→B→A 方向,以 1 cm/s 的速度运动至点 A 处,线段 DP 将△ABC 分成两部分,其中一部分与△ABC 相似,设运动时间为 t.
(1)当 P 在线段 BC 上运动时,BP= ______,当 P 在线段 AB 上运动时,BP= ______(请用含 t 的代数式表示)；
(2)求出满足条件的所有 t 值.

答案：
13.
(1)(6 - t)cm　(t - 6)cm
(2)如图
(1)，点P在线段BC上，当△CPD∽△CAB时，$\frac{CP}{CA}=\frac{CD}{CB}$，
∴$\frac{t}{3}=\frac{1}{6}$，
∴t=$\frac{1}{2}$.当△CDP'∽△CAB时，$\frac{CD}{CA}=\frac{CP'}{CB}$，
∴$\frac{1}{3}=\frac{t}{6}$，
∴t=2.
　　　　　　
　如图
(2)，点P在线段AB上，当△ADP∽△ACB时，$\frac{AP}{AB}=\frac{AD}{AC}$，
∴$\frac{10 - t}{4}=\frac{2}{3}$，
∴t=$\frac{22}{3}$.当△ADP'∽△ABC时，$\frac{AP'}{AC}=\frac{AD}{AB}$，
∴$\frac{10 - t}{3}=\frac{2}{4}$，
∴t=$\frac{17}{2}$.
　　　　　　
　综上所述，满足条件的t的值为$\frac{1}{2}$或2或$\frac{22}{3}$或$\frac{17}{2}$.

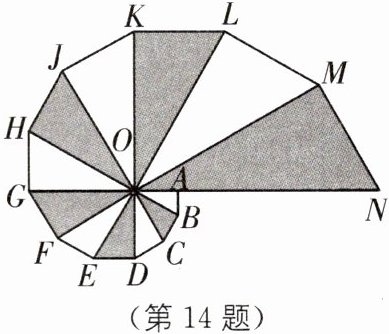
14. (2024·巴中中考)如图是用 12 个相似的直角三角形组成的图案. 若 OA= 1,则 OG= (C).

A.$\frac{125\sqrt{5}}{64}$
B.$\frac{125}{64}$
C.$\frac{64}{27}$
D.$\frac{32\sqrt{3}}{27}$

答案： 14.C　[解析]
∵图中12个直角三角形都相似，
∴每一个直角三角形中较小的锐角为360°÷12 = 30°.在Rt△OAB中，
∵∠AOB = 30°，
∴OB = 2AB，
∴OA=$\sqrt{OB^2 - AB^2}=\sqrt{(2AB)^2 - AB^2}=\sqrt{3}AB$，
∴$\frac{OA}{OB}=\frac{\sqrt{3}}{2}$.同理可得，$\frac{OB}{OC}=\frac{\sqrt{3}}{2}$，$\frac{OC}{OD}=\frac{\sqrt{3}}{2}$，$\frac{OD}{OE}=\frac{\sqrt{3}}{2}$，$\frac{OE}{OF}=\frac{\sqrt{3}}{2}$，$\frac{OF}{OG}=\frac{\sqrt{3}}{2}$，
∴$\frac{OA}{OG}=(\frac{\sqrt{3}}{2})^6=\frac{27}{64}$.又OA = 1，
∴OG=$\frac{64}{27}$.故选C.