《2025年实验班提优训练九年级数学上册浙教版》

1.(2024·广州中考)善于提问是应用人工智能解决问题的重要因素之一.为了解同学们的提问水平,对A,B两组同学进行问卷调查,并根据结果对每名同学的提问水平进行评分,得分情况如表(单位:分):
|A组|75|78|82|82|84|86|87|88|93|95|
|B组|75|77|80|83|85|86|88|88|92|96|
(1)求A组同学得分的中位数和众数;
(2)现从A,B两组得分超过90分的4名同学中随机抽取2名同学参与访谈,求这2名同学恰好来自同一组的概率.

答案：
1.
(1)由题意，得每组学生人数为10人，
∴中位数为第5,6名同学得分的平均数,
∴A组同学得分の中位数为$\frac{84 + 86}{2}=85$(分)
∵82分出现了两次次数最多,
∴众数为82分,
(②)由题意,得A,B两组得分超过90分的同学各有名,令A组的2名同学分别为$A_{1},A_{2}$,B组的2名同学分别为$B_{1},B_{2}$,画树状图如图。

共有12种等可能的结果,其中这2名同学恰好来自同一组的结果有4种,
∴这2名同学恰好来自同一组的概率为$\frac{4}{12}=\frac{1}{3}$。

2. 3月14日是国际数学日,某校在“国际数学日”当天举行了丰富多彩的数学活动,其中游戏类活动有:A. 数字猜谜;B. 数独;C. 魔方;D. 24点游戏;E. 数字华容道.该校为了解学生对这五类数学游戏的喜爱情况,随机抽取部分学生进行了调查统计(每位学生必选且只能选一类),并根据调查结果,绘制了两幅不完整的统计图如图所示.

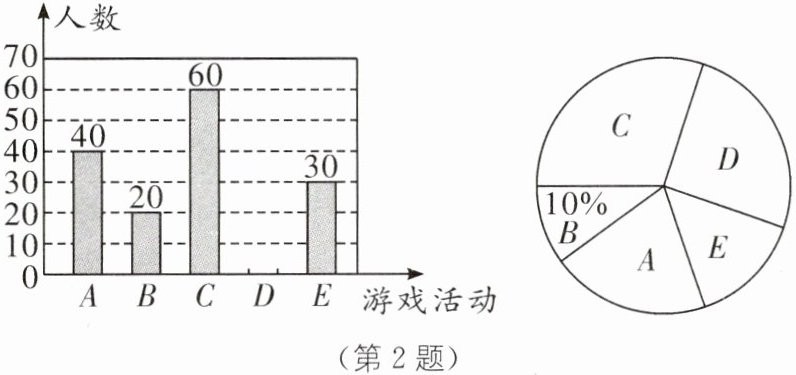
根据上述信息,解决下列问题.
(1)本次调查总人数为______人,A类活动所占圆心角的度数为______;
(2)补全条形统计图;(要求在条形图上方注明人数);
(3)若该校有2000名学生,请估计该校参加魔方游戏的学生人数;
(4)该校从C类中挑选出2名男生和2名女生,计划从这4名学生中随机抽取2名学生参加市青少年魔方比赛,恰好抽到1名男生和1名女生的概率是______.

答案：
2.
(1)200 72° [解析]$20÷10\% =200$(人),
∴本次调查总人数为200人。$40÷200×360^{\circ }=72^{\circ }$,
∴A类活动所占圆心角的度数为$72^{\circ }$。
(2)$200-(40+20+60+30)=50$(人),
∴喜欢24点游戏的有50人。补全条形统计图如图
(1)。

(3)$2000×\frac{60}{200}=600$(人),
∴该校参加魔方游戏的学生人数约为600人。
(4)根据题意,画树状图如图
(2)。

共有12种等可能的结果,恰好抽到1名男生和1名女生的结果有8种,
∴恰好抽到1名男生和1名女生的概率是$\frac{8}{12}=\frac{2}{3}$。

3. 从背面相同的同一副扑克牌中取出红桃9张,黑桃10张,方块11张,现将这些牌洗匀背面朝上放桌面上.
(1)求从中抽出一张是红桃的概率.
(2)现从桌面上先抽掉若干张黑桃,再放入与抽掉的黑桃张数相同的红桃,并洗匀且背面都朝上排开后,随机抽一张是红桃的概率不小于$\frac{2}{5}$,则至少抽掉了多少张黑桃?
(3)若先从桌面上抽掉9张红桃和$m(m＞6)$张黑桃后,再在桌面上抽出一张牌,当m为何值时,事件“再抽出的这张牌是方块”为必然事件?当m为何值时,事件“再抽出的这张牌是方块”为随机事件?请求出这个事件的概率的最小值.

答案： 3.
(1)抽出一张是红桃的概率是$\frac{9}{9+10+11}=\frac{3}{10}$。
(2)设抽掉了x张黑桃,放入x张红桃,根据题意,得$\frac{9+x}{9+10+11}\geq \frac{2}{5}$,解得$x\geq 3$。故至少抽掉了3张黑桃。
(3)当m为10时,事件"再抽出的这张牌是方块"为必然事件。当m为9,8,7时,事件"再抽出的这张牌是方块"为随机事件。当$m=9$时,$P=\frac{11}{(10-9)+11}=\frac{11}{12}$;当$m=8$时,$P=\frac{11}{(10-8)+11}=\frac{11}{13}$;当$m=7$时,$P=\frac{11}{(10-7)+11}=\frac{11}{14}$。又$\frac{11}{12}＞\frac{11}{13}＞\frac{11}{14}$,故从桌面上抽掉7张黑桃后,该事件的概率最小,最小值为$\frac{11}{14}$。