《2025年实验班提优训练九年级数学上册浙教版》

15. 中考新考法 添加条件开放 如图,四边形 ABCD 是$\odot O$的内接四边形,对角线 AC 与 BD 交于点 P,下面给出 5 个论断:①$AB// CD$;②$AP= PC$;③$AB= CD$;④$\angle BAD= \angle DCB$;⑤$AD// BC$.
(1)若用①和④论断作为条件,试证明四边形 ABCD 是矩形.
(2)请你另选取两个能推出四边形 ABCD 为矩形的论断,如①和③.(不证明,用序号表示即可)
(3)若选取论断③和⑤作为条件,能推出四边形 ABCD 为矩形吗? 若能,给出证明;若不能,举反例说明.
]

(1)∵四边形ABCD是⊙O的内接四边形,∴∠BAD+∠DCB=180°.又∠BAD=∠DCB,∴∠BAD=∠DCB=90°.∵AB//DC,∴∠BAD+∠ADC=180°,∴∠ADC=90°.∴四边形ABCD是矩形.(3)不能，反例：AD//BC,AB=DC,四边形ABCD是等腰梯形.

答案：
(1)
∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠DCB=180°.又∠BAD=∠DCB,
∴∠BAD=∠DCB=90°.
∵AB//DC,
∴∠BAD+∠ADC=180°,
∴∠ADC=90°.
∴四边形ABCD是矩形.
(2)答案不唯一,如:①　③
(3)不能，反例：AD//BC,AB=DC,四边形ABCD是等腰梯形.

16. 中考新考法 新定义问题 如图,A,B 是$\odot O$上的两个定点,P 是$\odot O$上的动点(点 P 不与点 A,B 重合),我们称$\angle APB是\odot O$上关于点 A,B 的滑动角.
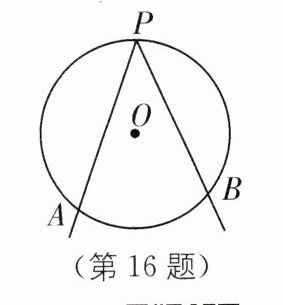
(1)已知$\angle APB是\odot O$上关于点 A,B 的滑动角.
①若 AB 是$\odot O$的直径,则$\angle APB= $______;
②若$\odot O$的半径是 1,$AB= \sqrt {2}$,求$\angle APB$的度数.
(2)若$\odot O$的半径是 1,$1\leq AB\leq \sqrt {2}$,求$\angle APB$的取值范围.
]

答案：

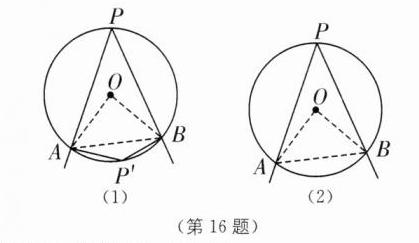
(1)①90°②如图
(1),连结OA,OB,AB.
∵⊙O的半径是1,即OA=OB=1,AB=$\sqrt{2}$,
∴由勾股定理的逆定理，得△OAB为直角三角形，且∠AOB=90°.当点P在优弧AB上时,∠APB=$\frac{1}{2}$∠AOB=45°;当点P'在劣弧AB上时,∠AP'B=$\frac{1}{2}$(360°−∠AOB)=135°.故∠APB的度数为45°或135°.
(2)如图
(2),连结OA,OB,AB.当AB=1时，
∵OA=OB=AB=1,
∴△OAB是等边三角形,
∴∠AOB=60°.当AB=$\sqrt{2}$时,
∵$AB^{2}=OA^{2}+OB^{2}=2$,
∴∠AOB=90°.①若点P在优弧上,∠APB=$\frac{1}{2}$∠AOB,
∴∠APB=30°或∠APB=45°,
∴30°≤∠APB≤45°;②若点P在劣弧上,∠APB=180°−30°=150°或∠APB=180°−45°=135°,
∴135°≤∠APB≤150°.综上所述,30°≤∠APB≤45°或135°≤∠APB≤150°.

17.(2024·浙江中考)如图,在圆内接四边形 ABCD 中,$AD＜AC$,$\angle ADC＜\angle BAD$,延长 AD 至点 E,使$AE= AC$,延长 BA 至点 F,连结 EF,使$\angle AFE= \angle ADC$.
(1)若$\angle AFE= 60^{\circ }$,CD 为直径,求$\angle ABD$的度数.
(2)求证:①$EF// BC$;②$EF= BD$.
]

答案：
(1)
∵CD为直径,
∴∠CAD=90°.
∵∠AFE=∠ADC=60°,
∴∠ACD=90°−60°=30°,
∴∠ABD=∠ACD=30°.
(2)①如图,延长AB.
∵四边形ABCD是圆内接四边形,
∴∠CBM=∠ADC.又∠AFE=∠ADC,
∴∠AFE=∠CBM,
∴EF//BC.②如图，过点D作DG//BC交⊙O于点G,连结AG,CG.
∵DG//BC,
∴$\overset{\frown}{BD}=\overset{\frown}{CG}$,
∴BD=CG.
∵四边形ACGD是圆内接四边形,
∴∠GDE=∠ACG.
∵EF//DG,
∴∠DEF=∠GDE,
∴∠DEF=∠ACG.
∵∠AFE=∠ADC,∠ADC=∠AGC,
∴∠AFE=∠AGC.
∵AE=AC,
∴△AEF≌△ACG(AAS),
∴EF=CG,
∴EF=BD.