《2025年实验班提优训练九年级数学上册浙教版》

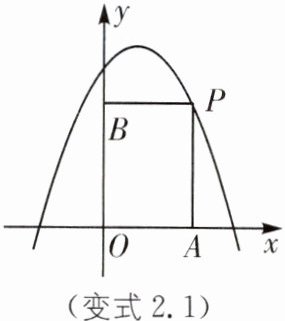
变式2.1 (2025·吉林长春期末)如图,$P是抛物线y= -x^{2}+x+3$在第一象限内的点,过点$P分别向x轴和y$轴作垂线,垂足分别为$A,B$,则四边形$OAPB$周长的最大值为(C).

A.6
B.7
C.8
D.9

答案： C [解析]令y = 0,则 - x²+x + 3 = 0,解得x = $\frac{1±\sqrt{13}}{2}$,
∴抛物线与x轴正半轴交于点($\frac{1+\sqrt{13}}{2}$,0).
设P(x, - x²+x + 3)(0＜x＜$\frac{1+\sqrt{13}}{2}$),
四边形OAPB的周长 = 2PA + 2OA = - 2x²+2x + 6+2x = - 2x²+4x + 6 = - 2(x - 1)²+8,
当x = 1时,四边形OAPB周长有最大值，最大值为8.故选C.

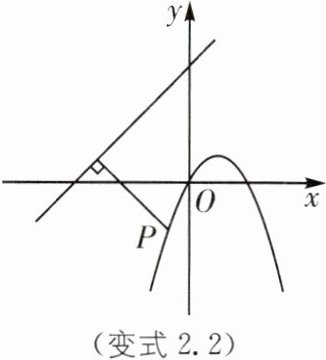
变式2.2 (陕西西安交大附中自主招生)如图,一次函数$y_{1}= x+4,y_{2}= -x^{2}+2x$,$P为y_{2}$上一动点,求$P到y_{1}$的距离的最小值.

答案： 如图,过点P作PH⊥y₁,垂足为H,作PQ//y轴，交y₁于点Q,A,B分别为y₁与x轴,y轴交点.
设P(t, - t²+2t),则Q(t,t + 4),
∴PQ = t + 4 - ( - t²+2t)=t² - t + 4.
令x = 0,y₁ = 4;令y₁ = 0,x = - 4,
∴A( - 4,0),B(0,4),
∴OA = OB,
∴△AOB是等腰直角三角形,∠ABO = 45°.
∵PQ//y轴,
∴∠PQH = ∠ABO = 45°.
∵PH⊥y₁,
∴∠PHQ = 90°,
∴△PHQ是等腰直角三角形,
∴PH = QH,
∴PQ² = PH²+QH² = 2PH²,
∴PH = $\frac{\sqrt{2}}{2}$PQ = $\frac{\sqrt{2}}{2}$(t² - t + 4)= $\frac{\sqrt{2}}{2}$(t - $\frac{1}{2}$)²+$\frac{15\sqrt{2}}{8}$,
∴当t = $\frac{1}{2}$时,PH有最小值,最小值为$\frac{15\sqrt{2}}{8}$.

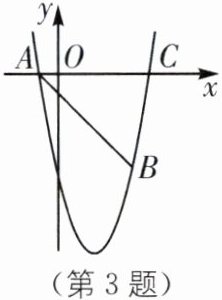
3. 如图,抛物线$y= ax^{2}+bx+c(a,b,c$为常数,$a≠0)经过点A(-1,0),B(5,-6),C(6,0)$.
(1)求抛物线的表达式；
(2)如图,连结$AB$,点$P在直线AB$下方的抛物线上,求出$\triangle ABP的面积取最大时点P$的坐标.

答案：
(1)由题可设y = a(x + 1)(x - 6)(a≠0)，
把B(5, - 6)代入，
得a(5 + 1)(5 - 6)= - 6,解得a = 1，
∴y = (x + 1)(x - 6)=x² - 5x - 6.
(2)如图,连结AP,BP,过点P作PD⊥x轴于点D,交AB于点E,
设直线AB的表达式为y = kx + n，
将A( - 1,0),B(5, - 6)代入,
得$\begin{cases}-k + n = 0, \\5k + n = - 6,\end{cases}$解得$\begin{cases}k = - 1, \\n = - 1.\end{cases}$
∴直线AB的表达式为y = - x - 1.
设P(m,m² - 5m - 6)( - 1＜m＜5),
则E(m, - m - 1),
∴PE = ( - m - 1) - (m² - 5m - 6)= - m²+4m + 5,
∴S_{△ABP} = $\frac{1}{2}$PE·(x_{B}-x_{A}) = $\frac{1}{2}$( - m²+4m + 5)×6 = - 3(m - 2)²+27,
∴当m = 2时,S_{△ABP}最大,此时P(2, - 12).

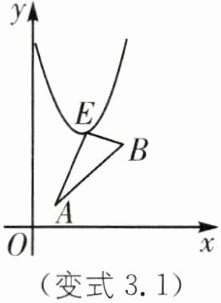
变式3.1 实验班原创 如图,点$A,B是直线y= x$在第一象限中的两点,横坐标分别为$a,a+3$,若点$E是抛物线y= x^{2}-4x+8$上的一点,连结$EA,EB$,求$\triangle ABE$面积的最小值.

答案： 设点E(m,m² - 4m + 8),如图,过点E作EM垂直于x轴交AB于点M,作BF⊥EM,AG⊥EM,垂足分别为F,G，
由题意,得M(m,m),
∴EM = m² - 4m + 8 - m = m² - 5m + 8 = (m - $\frac{5}{2}$)²+$\frac{7}{4}$,
∴S_{△ABE} = S_{△AEM}+S_{△EMB} = $\frac{1}{2}$EM·AG + $\frac{1}{2}$EM·BF = $\frac{1}{2}$EM(AG + BF)= $\frac{3}{2}$(m - $\frac{5}{2}$)²+$\frac{21}{8}$.
∵$\frac{3}{2}$＞0,
∴S_{△ABE}有最小值,
∴当m = $\frac{5}{2}$时,S_{△ABE}的最小值为$\frac{21}{8}$.

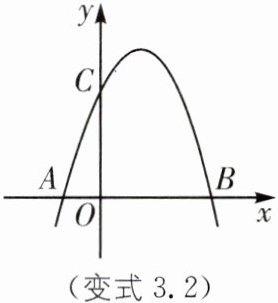
变式3.2 (2024·湖北荆门期中)如图,已知抛物线$y= -x^{2}+2x+3与y轴交于点C$,与$x轴交于A,B$两点(点$A在点B$左边).
(1)请直接写出$A,B,C$三点的坐标；
(2)若点$P$是第一象限内抛物线上一点,求$\triangle PBC面积最大时点P$的坐标.

答案：
(1)当x = 0时,y = 3,
∴C(0,3).
当y = 0时, - x²+2x + 3 = 0,
解得x₁ = 3,x₂ = - 1,
∴A( - 1,0),B(3,0).
(2)如图,过点P作PN⊥x轴于点N,交BC于点D,连结PB,PC,
则S_{△BCP} = $\frac{1}{2}$PD·OB.
∵B(3,0),
∴OB = 3,
∴S_{△BCP} = $\frac{1}{2}$PD·OB = $\frac{3}{2}$PD.
设直线BC的表达式为y = kx + b,把B(3,0),C(0,3)代入,得$\begin{cases}0 = 3k + b, \\3 = b,\end{cases}$解得$\begin{cases}k = - 1, \\b = 3.\end{cases}$
∴直线BC的表达式为y = - x + 3.
设D(m, - m + 3),P(m, - m²+2m + 3),0＜m＜3,
∴PD = - m²+2m + 3 - ( - m + 3)= - m²+3m = - (m - $\frac{3}{2}$)²+$\frac{9}{4}$,
∴当m = $\frac{3}{2}$时,PD取最大值,此时△BCP的面积最大，
∴P($\frac{3}{2}$,$\frac{15}{4}$).