第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
1.(2024·天津河西区期末)抛物线$y= x^{2}-2x-3$与x轴的两个交点的坐标分别为(
A.$(3,0),(-1,0)$
B.$(-3,0),(1,0)$
C.$(2,0),(-4,0)$
D.$(4,0),(-2,0)$
A
).A.$(3,0),(-1,0)$
B.$(-3,0),(1,0)$
C.$(2,0),(-4,0)$
D.$(4,0),(-2,0)$
答案:
A [解析]当y=0时,x²−2x−3=0,解得x₁=−1,x₂=3,所以抛物线y=x²−2x−3与x轴的两个交点的坐标分别为(−1,0),(3,0).故选A.
2. 教材 P29例5·变式 下表是若干组二次函数$y= x^{2}-5x+c$的自变量x与函数值y的对应值:
| x | ... | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | ... |
| y | ... | 0.36 | 0.13 | -0.08 | -0.27 | -0.44 | ... |
那么方程$x^{2}-5x+c= 0$的一个近似根(精确到0.1)是(
A.3.4
B.3.5
C.3.6
D.3.7
| x | ... | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | ... |
| y | ... | 0.36 | 0.13 | -0.08 | -0.27 | -0.44 | ... |
那么方程$x^{2}-5x+c= 0$的一个近似根(精确到0.1)是(
B
).A.3.4
B.3.5
C.3.6
D.3.7
答案:
B [解析]
∵二次函数y=x²−5x+c,
∴对称轴为直线x=$\frac{5}{2}$.观察表格,得方程x²−5x+c=0的一个近似根(精确到0.1)是1.5,
∴另一个近似根m满足$\frac{m + 1.5}{2}$ = $\frac{5}{2}$,
∴m = 3.5.故选B
方法诠释 根据二次函数的图象的对称性,由一个根可以求得另一个根.
∵二次函数y=x²−5x+c,
∴对称轴为直线x=$\frac{5}{2}$.观察表格,得方程x²−5x+c=0的一个近似根(精确到0.1)是1.5,
∴另一个近似根m满足$\frac{m + 1.5}{2}$ = $\frac{5}{2}$,
∴m = 3.5.故选B
方法诠释 根据二次函数的图象的对称性,由一个根可以求得另一个根.
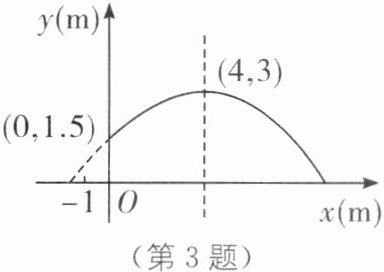
3.(2025·绍兴上虞区期末)一运动员推铅球,铅球经过的路线为如图所示的抛物线(实线部分).根据图中相关信息,你认为铅球的落地点与该运动员相距大约在(
A.在8m~9m之间
B.在9m~10m之间
C.在10m~11m之间
D.在11m~12m之间
B
).
A.在8m~9m之间
B.在9m~10m之间
C.在10m~11m之间
D.在11m~12m之间
答案:
B [解析]由图可知抛物线的顶点坐标为(4,3),图象过点(0,1.5)
∴设抛物线的表达式为y=a(x−4)²+3.把(0,1.5)代入得,1.5=a(0−4)²+3,解得a=−$\frac{3}{32}$,
∴铅球所经过路线的函数表达式为y=−$\frac{3}{32}$(x−4)²+3.令y=0得,0=−$\frac{3}{32}$(x−4)²+3,解得x₁=4 + 4$\sqrt{2}$,x₂=4 - 4$\sqrt{2}$(舍去),
∵1.96<2<2.25,
∴1.4<$\sqrt{2}$<1.5,
∴9.6<4 + 4$\sqrt{2}$<10,
∴铅球的落地点与该运动员相距大约在9m~10m之间.故选B.
∴设抛物线的表达式为y=a(x−4)²+3.把(0,1.5)代入得,1.5=a(0−4)²+3,解得a=−$\frac{3}{32}$,
∴铅球所经过路线的函数表达式为y=−$\frac{3}{32}$(x−4)²+3.令y=0得,0=−$\frac{3}{32}$(x−4)²+3,解得x₁=4 + 4$\sqrt{2}$,x₂=4 - 4$\sqrt{2}$(舍去),
∵1.96<2<2.25,
∴1.4<$\sqrt{2}$<1.5,
∴9.6<4 + 4$\sqrt{2}$<10,
∴铅球的落地点与该运动员相距大约在9m~10m之间.故选B.
4. 已知方程$2x^{2}-3x-5= 0的两根是\frac {5}{2},-1$,则二次函数$y= 2x^{2}-3x-5$的图象与x轴的两个交点间的距离为
3.5
.
答案:
3.5
5.(2025·温州鹿城区期末)设抛物线$y= ax^{2}-2x-3与直线y= 2x-3交于点A(4,b).$
(1)求抛物线的表达式及其对称轴;
(2)设点$B(x_{1},y_{1}),C(x_{2},y_{2})$是抛物线上两点,且位于对称轴两侧,$x_{2}-x_{1}= 3.$
①若$y_{1}= y_{2}$,求$x_{1}$的值;
②直线 BC 与直线$y= 2x-3交于点D(x_{3},y_{3})$,且$y_{1}<y_{3}<y_{2}$,直接写出$x_{1}$的取值范围.
(1)求抛物线的表达式及其对称轴;
(2)设点$B(x_{1},y_{1}),C(x_{2},y_{2})$是抛物线上两点,且位于对称轴两侧,$x_{2}-x_{1}= 3.$
①若$y_{1}= y_{2}$,求$x_{1}$的值;
②直线 BC 与直线$y= 2x-3交于点D(x_{3},y_{3})$,且$y_{1}<y_{3}<y_{2}$,直接写出$x_{1}$的取值范围.
答案:
(1)将A(4,b)代入y=2x−3,得b=5,
∴A(4,5).将A(4,5)代入y=ax²−2x−3,得a=1,
∴y=x²−2x−3.
∵y=x²−2x−3=(x−1)²−4,
∴对称轴为直线x=1.
(2)①
∵y₁=y₂,
∴点B,点C关于对称轴对称,
∴$\frac{x₁ + x₂}{2}$ = 1.
∵x₂ - x₁ = 3,
∴x₁ = −$\frac{1}{2}$.
②由图象,得当−$\frac{1}{2}$<x₁<0时,y₁<y₃<y₂.
(1)将A(4,b)代入y=2x−3,得b=5,
∴A(4,5).将A(4,5)代入y=ax²−2x−3,得a=1,
∴y=x²−2x−3.
∵y=x²−2x−3=(x−1)²−4,
∴对称轴为直线x=1.
(2)①
∵y₁=y₂,
∴点B,点C关于对称轴对称,
∴$\frac{x₁ + x₂}{2}$ = 1.
∵x₂ - x₁ = 3,
∴x₁ = −$\frac{1}{2}$.
②由图象,得当−$\frac{1}{2}$<x₁<0时,y₁<y₃<y₂.
6.(2024·杭州萧山区高桥初中月考)如图,一次函数$y_{1}= x与二次函数y_{2}= ax^{2}+bx+c$的图象相交于P,Q两点,则关于一元二次方程$ax^{2}+(b-1)x+c= 0$的根的说法正确的是(
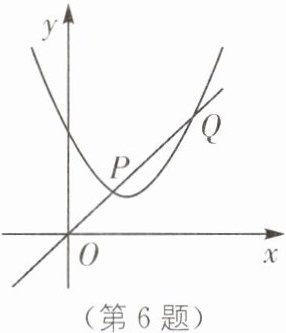
A.有两个负根
B.有两个正根
C.有一正一负的两根
D.无实数根
B
).
A.有两个负根
B.有两个正根
C.有一正一负的两根
D.无实数根
答案:
B[解析]
∵一次函数y₁=x与二次函数y₂=ax²+bx+c的图象相交于P,Q两点,
∴一元二次方程ax²+(b−1)x + c=0有两个不相等的实数根,
∵P,Q两点在第一象限,
∴一元二次方程ax²+(b−1)x + c=0有两个不相等的正实数根.故选B.
∵一次函数y₁=x与二次函数y₂=ax²+bx+c的图象相交于P,Q两点,
∴一元二次方程ax²+(b−1)x + c=0有两个不相等的实数根,
∵P,Q两点在第一象限,
∴一元二次方程ax²+(b−1)x + c=0有两个不相等的正实数根.故选B.
7.(2024·绍兴上虞区期末)点$A(1,m),B(3,n)在抛物线y= ax^{2}+bx+4(a>0)$上,设抛物线的对称轴为直线$x= t$,若$m<n<4$,则t的取值范围是(
A.$\frac {1}{2}<t<2$
B.$2<t<3$
C.$\frac {3}{2}<t<2$
D.$1<t<2$
C
).A.$\frac {1}{2}<t<2$
B.$2<t<3$
C.$\frac {3}{2}<t<2$
D.$1<t<2$
答案:
C [解析]
∵m<n<4,
∴a + b + 4<9a + 3b + 4<4,解得−4a<b<−3a,
∴3a<−b<4a,
∴$\frac{3a}{2a}$<−$\frac{b}{2a}$<$\frac{4a}{2a}$.
∵抛物线的对称轴为直线x=t,即t=−$\frac{b}{2a}$,
∴$\frac{3}{2}$<t<2.故选C.
∵m<n<4,
∴a + b + 4<9a + 3b + 4<4,解得−4a<b<−3a,
∴3a<−b<4a,
∴$\frac{3a}{2a}$<−$\frac{b}{2a}$<$\frac{4a}{2a}$.
∵抛物线的对称轴为直线x=t,即t=−$\frac{b}{2a}$,
∴$\frac{3}{2}$<t<2.故选C.
8. 已知函数$y= \left\{\begin{array}{l} (x-3)^{2}-1(x≤5),\\ (x-7)^{2}-1(x>5)\end{array} \right. 若使y= k$成立的x值恰好有三个,则k的值为______
3
.
答案:
3 [解析]函数y = { (x - 3)² - 1 (x ≤ 5), (x - 7)² - 1 (x > 5) }的图象如图.根据图象可知当y=3时,对应成立的x值恰好有三个,
∴k=3.
方法诠释 先画出函数图象,再利用数形结合的方法即可找到使y=k成立的x值恰好有三个的k值.
∴k=3.
方法诠释 先画出函数图象,再利用数形结合的方法即可找到使y=k成立的x值恰好有三个的k值.
查看更多完整答案,请扫码查看


