《2025年实验班提优训练九年级数学上册浙教版》

1. 如图,等边三角形ABC的边长为3,P为BC上一点,且BP= 1,D为AC上一点,若∠APD= 60°,则CD的长为(B).

A.$\frac{3}{2}$
B.$\frac{2}{3}$
C.$\frac{1}{2}$
D.$\frac{3}{4}$

答案： B

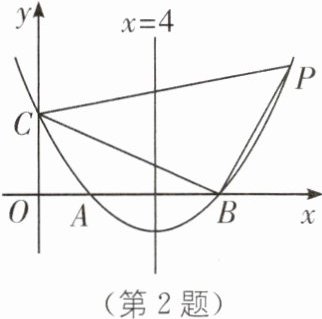
2. 如图,已知抛物线的对称轴是直线$x= 4$,该抛物线与x轴交于A,B两点,与y轴交于C点,且A,C点的坐标分别是(2,0),(0,3).
(1)求抛物线的函数表达式.
(2)抛物线上有一点P,满足∠PBC= 90°,求点P的坐标.

答案：

(1)设抛物线的表达式是$y=a(x - 4)^{2}+b$，根据题意，得$\left\{\begin{array}{l} 4a + b = 0\\ 16a + b = 3\end{array}\right.$，解得$\left\{\begin{array}{l} a = \frac{1}{4}\\ b = -1\end{array}\right.$。
则抛物线的表达式是$y = \frac{1}{4}x^{2}-2x + 3$。
(2)如图，过P作$PF⊥x$轴于点F，则$\triangle PBF\backsim \triangle BCO$，$\therefore \frac{PF}{BF}=\frac{OB}{OC}=\frac{6}{3}=2$，$\therefore$设点P的坐标为$(m,n)$，则$n = 2(m - 6)$①。
又点P在抛物线上，$\therefore n = \frac{1}{4}m^{2}-2m + 3$②，
①②联立，解得$m_1 = 10$，$m_2 = 6$（舍去），
$\therefore n = 2×(10 - 6)=8$，
$\therefore$点P的坐标为$P(10,8)$。

3.(2025·重庆綦江区期末)通过对如图数学模型的研究学习,解决下列问题：
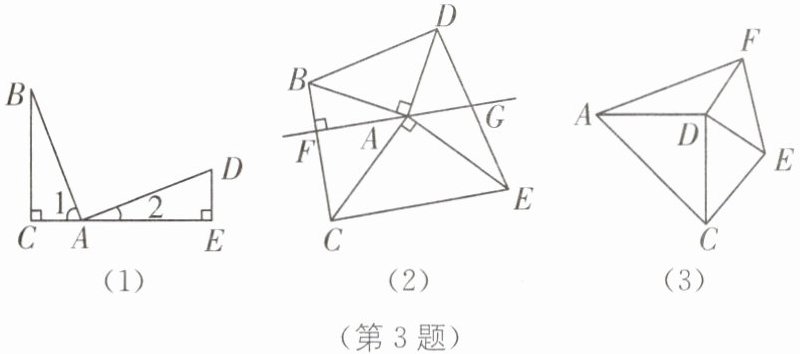
(1)如图(1),∠BAD= 90°,AB= AD,过点B作BC⊥AC于点C,过点D作DE⊥AC于点E.由∠1+∠2= ∠2+∠D= 90°,得∠1= ∠D.又∠ACB= ∠AED= 90°,可以推理得到△ABC≌△DAE.进而得到AC= ,BC= ,BC+DE= .我们把这个数学模型称为“K字”模型或“一线三等角”模型；
(2)如图(2),∠BAD= ∠CAE= 90°,AB= AD,AC= AE,连结BC,DE,且BC⊥AF于点F,DE与直线AF交于点G.求证：点G是DE的中点；(我们把这个数学模型称为“婆罗摩笈多”模型)
(3)如图(3),∠ADC= ∠EDF= 90°,AD= DC,DE= DF,连结AC,EF,△AFD的面积为$S_1,△DCE$的面积为$S_2,S_1+S_2= 2024,$求$S_2$的值.

答案：

(1)DE AE CE [解析]$\because BC⊥AC$，$DE⊥AC$，
$\therefore \angle ACB = \angle DEA = 90^{\circ}=\angle BAD$，
$\therefore \angle 1 + \angle 2 = \angle 2 + \angle D = 90^{\circ}$，
$\therefore \angle 1 = \angle D$。
在$\triangle ABC$和$\triangle DAE$中，$\left\{\begin{array}{l} \angle ACB = \angle DEA = 90^{\circ}\\ \angle 1 = \angle D\\ AB = DA\end{array}\right.$
$\therefore \triangle ABC\cong \triangle DAE(AAS)$，
$\therefore AC = DE$，$BC = AE$，
$\therefore BC + DE = AE + AC = CE$。
(2)如图
(1)，过D作$DM⊥AF$于M，过E作$EN⊥AF$于N，

由“K字”模型得，$\triangle ABF\cong \triangle DAM(AAS)$，
$\therefore AF = DM$，
同理$AF = EN$，
$\therefore EN = DM$；
$\because DM⊥AF$，$EN⊥AF$，
$\therefore \angle GMD = \angle GNE = 90^{\circ}$。
在$\triangle DMG$与$\triangle ENG$中，
$\left\{\begin{array}{l} \angle DMG = \angle ENG = 90^{\circ}\\ \angle DGM = \angle EGN\\ DM = EN\end{array}\right.$
$\therefore \triangle DMG\cong \triangle ENG(AAS)$，
$\therefore DG = EG$，
$\therefore$点G是DE的中点。
(3)$\angle ADC = \angle EDF = 90^{\circ}$，$AD = DC$，$DE = DF$，如图
(2)，过D作$PQ⊥CE$于P，交AF于Q，过A作$AM⊥PQ$于M，过F作$FN⊥PQ$于N，

由“K字”模型得$\triangle ADM\cong \triangle DCP(AAS)$，$\triangle DFN\cong \triangle EDP(AAS)$，
$\therefore S_{\triangle ADM}=S_{\triangle DCP}$，$S_{\triangle DFN}=S_{\triangle EDP}$，
由
(2)知，点Q是AF的中点，得$\triangle AMQ\cong \triangle FNQ(AAS)$，
$\therefore S_{\triangle AMQ}=S_{\triangle FNQ}$，
$\therefore S_{\triangle AFD}=S_{\triangle ADQ}+S_{\triangle FNQ}+S_{\triangle DFN}=S_{\triangle ADQ}+S_{\triangle AMQ}+S_{\triangle DFN}=S_{\triangle ADM}+S_{\triangle DFN}=S_{\triangle DCP}+S_{\triangle EDP}=S_{\triangle CDE}$。
$\because \triangle AFD$的面积为$S_1$，$\triangle DCE$的面积为$S_2$，即$S_1 = S_2$，
$\because S_1 + S_2 = 2024$，
$\therefore S_2$的值为1012。