《2025年实验班提优训练九年级数学上册浙教版》

11. 如图,在矩形$ ABCD $中,已知$ AB= 8 $,$ BC= 6 $,矩形在直线$ l $上绕其右下角的顶点 B 顺时针旋转 90° 至图①位置,再绕其右下角的顶点继续顺时针旋转$ 90^{\circ} $至图②位置,……,以此类推,这样连续旋转 2025 次后,顶点$ A $在整个旋转过程中所经过的路程之和为6076π.

答案： 6076π　[解析]在矩形ABCD中,
∵AB=8,BC=6,
∴AC=BD=$\sqrt{6^2+8^2}$=10,
∴转动第一次A的路线长是$2\pi×8×\frac{90}{360}$=4π,转动第二次A的路线长是$2\pi×10×\frac{90}{360}$=5π,转动第三次A的路线长是$2\pi×6×\frac{90}{360}$=3π,转动第四次A的路线长是0,以此类推，每4次一循环故顶点A转动4次经过√的路线总长为4π+5π+3π+0=12π.
∵2025÷4=506……1,
∴连续旋转2025次后，顶点A在整个旋转过程中所经过的路程之和为506×12π+4π=6076π归纳总结　本题主要考查了轨迹、矩形的性质、旋转变换的性质、勾股定理和弧长公式的运用，掌握旋转变换的性质、灵活运用弧长的计算公式、发现规律是解题的关键.

12. 如图,$ \triangle ABC $是等腰直角三角形,$ \angle ACB= 90^{\circ} $,$ AC= BC= 4 $,点$ D 是斜边 AB $上一点,且$ BD= \frac{1}{4}AB $,将$ \triangle ABC 绕点 D 逆时针旋转 90^{\circ} $,得到$ \triangle A'B'C' $,$ B'C' 交 AB 于点 E $. 其中点$ C 的运动路径为弧 CC' $,则弧$ CC' $的长度为 .

答案：
$\frac{\sqrt{10}\pi}{2}$　[解析]如图，连结CD,DC'，过点C作CH⊥AB 于点H.
∵AC=BC=4,∠ACB=90°,
∴AB=$4\sqrt{2}$,CH=BH=$2\sqrt{2}$.
∵BD=$\frac{1}{4}$AB,
∴BD=$\sqrt{2}$,
∴DH=$\sqrt{2}$.在Rt△CHD中,由勾股定理得CD=$\sqrt{CH^2+DH^2}=\sqrt{10}$,
∴弧CC'的长度为$\frac{90\pi×\sqrt{10}}{180}=\frac{\sqrt{10}\pi}{2}$.归纳总结　本题主要考查了等腰直角三角形的性质、勾股定理、旋转的性质等知识，熟练掌握弧长公式是解题的关键.

13. 如图,在$ \text{Rt}\triangle POQ $中,$ \angle POQ= 90^{\circ} $,$ \angle P= 30^{\circ} $,$ PQ= 6 $,将$ \text{Rt}\triangle POQ 绕点 O 逆时针旋转得到 \text{Rt}\triangle P'OQ' $,点$ Q 恰好落在斜边 P'Q' $上,则点$ P $经过的路径长为$\sqrt{3}\pi$.

答案： $\sqrt{3}\pi$　[解析]
∵将Rt△POQ绕点O逆时针旋转得到Rt△P'O'Q',
∴旋转角∠Q'OQ=∠POP',OQ=OQ',OP=OP'.
∵Rt△POQ中,∠POQ=90°,∠P=30°,PQ=6,
∴∠PQO=∠P'Q'O=60°,OQ=3,OP=$3\sqrt{3}$,
∴△OQ'Q是等边三角形,
∴∠POP'=∠Q'OQ=60°,
∴点P经过的路径长为$\frac{60\pi×3\sqrt{3}}{180}=\sqrt{3}\pi$.

14. (2024·义乌东阳期中)如图,量角器的直径与直角三角板$ ABC 的斜边 AB $重合($ AB= 6 $),其中量角器 0 刻度线的端点$ N 与点 A $重合,射线$ CP 从 CA $处出发沿顺时针方向以每秒 3 度的速度旋转,$ CP 与量角器的半圆弧交于点 E $,第 20 秒时点$ E $在量角器上的运动路径长是 2π.

答案： 2π　[解析]连结OE.
∵∠ACB=90°,
∴A,B,C在以点O为圆心,AB为直径的圆上，
∴点E,A,B,C共圆.
∵∠ACE=3°×20=60°,
∴∠AOE=2∠ACE=120°.
∴点E在量角器上的运动路径长为$\frac{120\pi×3}{180}$=2π.

15. (2025·河北秦皇岛期中改编)如图,在$ \triangle ABC $中,$ CA= CB $,以$ BC 为直径的 \odot O 分别与 AB $,$ AC 相交于点 D $,$ E $,过点$ D 作 DF\perp AC $,垂足为$ F $. 分别延长$ CB $,$ FD 相交于点 G $,$ \angle A= 60^{\circ} $,$ \odot O $的半径为 6,求阴影部分的周长.

答案：
如图，连结OD.
∵OB=OD,
∴∠ABC=∠ODB.
∵AC=BC,
∴∠ABC=∠BAC,
∴∠ODB=∠BAC.
∴OD//AC.
∵DF⊥AC,
∴DF⊥OD.
∵∠A=60°,AC=BC,
∴△ABC是等边三角形,
∴∠ACB=60°,
∴∠DOB=∠ACB=60°.
∵OD=OB=6,∠DOB=60°,
∴∠G=90°-∠BOD=60°,
∴OG=2OD=12,
∴DG=$\sqrt{OG^2-OD^2}=6\sqrt{3}$,BG=OG-OB=6.
∴弧BD的长=$\frac{60\pi×6}{180}=2\pi$,
∴阴影部分的周长=DG+BG+弧BD的长度=$6\sqrt{3}+6+2\pi$.

16. (2024·广东东莞长安实验中学期末)如图,在边长为 1 的正方形组成的网格中,$ \triangle AOB $的顶点均在格点上,点$ A $,$ B 的坐标分别是 A(3,2) $,$ B(1,3) $.
(1)画出$ \triangle AOB 绕点 O 逆时针旋转 90^{\circ} 后得到的 \triangle A_1OB_1 $,并写出$ A_1 $的坐标；
(2)在旋转过程中,点$ B 经过的路径为弧 BB_1 $,求弧$ BB_1 $的长.

答案：

(1)如图,A₁(-2,3).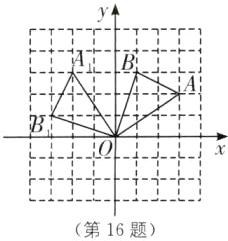
(2)由勾股定理，得OB=$\sqrt{3^2+1^2}=\sqrt{10}$,弧BB₁的长=$\frac{90\pi×\sqrt{10}}{180}=\frac{\sqrt{10}}{2}\pi$.