第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
6. 教材 P26 例 3·变式 (2024·浙江师大附中期中)某超市以每件 10 元的价格购进一种文具,销售该文具时,销售单价不低于进价且不高于 21 元.经过市场调查发现,该文具的每天销售数量 y(件)与销售单价 x(元)之间满足 $ y= -2x+60 $,则销售该文具每天获得的最大利润是
200
元.
答案:
200 [解析] 设销售该文具每天获得的利润为w元,根据题意,得$ w=(x-10)(-2x+60)=-2x^{2}+80x-600=-2(x-20)^{2}+200(10≤x≤21) $.
∵-2<0,
∴当$ x=20 $时,w有最大值,且最大值为200,
∴销售该文具每天获得的最大利润是200元.
∵-2<0,
∴当$ x=20 $时,w有最大值,且最大值为200,
∴销售该文具每天获得的最大利润是200元.
7. 某快餐店销售 A,B 两种快餐,每份利润分别为 12 元,8 元,该店为了增加利润,准备降低每份 A 种快餐的利润,同时提高每份 B 种快餐的利润.售卖时发现,在一定范围内,每份 A 种快餐利润每降 1 元可多卖 2 份,每份 B 种快餐利润每提高 1 元就少卖 2 份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是______元.
1264
答案:
1264 [解析] 设每份A种快餐降价a元,则每天卖出(40+2a)份,每份B种快餐涨价b元,则每天卖出(80-2b)份.由题意,得40+2a+80-2b=40+80,解得a=b.
∴总利润$ W=(12-a)(40+2a)+(8+a)·(80-2a)=-4a^{2}+48a+1120=-4(a-6)^{2}+1264 $.
∵-4<0,
∴当$ a=6 $时,W取得最大值为1264,即两种快餐一天的总利润最多是1264元.
∴总利润$ W=(12-a)(40+2a)+(8+a)·(80-2a)=-4a^{2}+48a+1120=-4(a-6)^{2}+1264 $.
∵-4<0,
∴当$ a=6 $时,W取得最大值为1264,即两种快餐一天的总利润最多是1264元.
8. (2025·杭州观城实验学校月考改编)中国传统手工艺品,如中国结、油纸伞、团扇等,是先民智慧和勤劳的结晶,是中华传统文化的表达方式之一,也是各地传统风俗的体现.某工艺品店购进一批团扇,每把进价为 20 元,按每把 25 元销售,每月可售出 210 把.现店方想采用提高售价的方法来增加利润(售价不超过 32 元).经试验,每把团扇的售价每提高 1 元,每月就会少卖出 10 把.请问:商家将该团扇每个的售价定为______元时,能使每月获利最大,最大利润是______元.
32
1680
答案:
32 1680 [解析] 设每把团扇售价为x元,每月团扇销售量为y把,每月销售利润为w元.根据题意,基础销售量为210件,提价销售减少量为10(x-25),根据题意,得$ y=210-10(x-25)=-10x+460 $,$ w=(x-20)(-10x+460)=-10(x-33)^{2}+1690 $.
∵-10<0,
∴当x<33时,w随x的增大而增大.
∵$ x≤32 $,
∴当$ x=32 $时,w取得最大值,为$ -10×(32-33)^{2}+1690=1680 $.故当每把团扇的售价定为32元时,每月的销售利润最大,最大利润为1680元.
∵-10<0,
∴当x<33时,w随x的增大而增大.
∵$ x≤32 $,
∴当$ x=32 $时,w取得最大值,为$ -10×(32-33)^{2}+1690=1680 $.故当每把团扇的售价定为32元时,每月的销售利润最大,最大利润为1680元.
9. (2025·上海黄浦区一模)如图,体育课上投掷实心球活动.小明某次投掷实心球,实心球出手后的运动过程中距离地面的高度 y(米)关于水平距离 x(米)的函数表达式为 $ y= -\frac{1}{8}x^{2}+bx+c $,当实心球运动到点 B 时达到最高点,那么实心球的落地点 C 与出手点 A 的水平距离 OC 为______米.
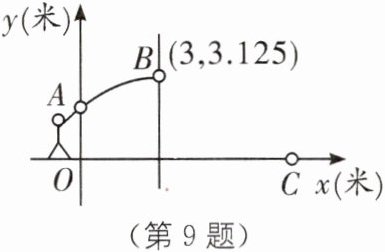

8
答案:
8 [解析]
∵实心球运动到点B(3,3.125)时达到最高点,
∴该二次函数表达式为$ y=-\frac{1}{8}(x-3)^{2}+3.125 $,
∴二次函数的表达式为$ y=-\frac{1}{8}x^{2}+\frac{3}{4}x+2 $,令$ y=0 $,则$ -\frac{1}{8}x^{2}+\frac{3}{4}x+2=0 $,解得$ x_{1}=8,x_{2}=-2 $(舍去).
∴实心球的落地点C与出手点A的水平距离OC为8米.
∵实心球运动到点B(3,3.125)时达到最高点,
∴该二次函数表达式为$ y=-\frac{1}{8}(x-3)^{2}+3.125 $,
∴二次函数的表达式为$ y=-\frac{1}{8}x^{2}+\frac{3}{4}x+2 $,令$ y=0 $,则$ -\frac{1}{8}x^{2}+\frac{3}{4}x+2=0 $,解得$ x_{1}=8,x_{2}=-2 $(舍去).
∴实心球的落地点C与出手点A的水平距离OC为8米.
10. 新情境 汽车制动 (2025·杭州临平区月考)汽车的制动距离是衡量一款车的制动性能的关键性参数之一,它的意思是在车辆处于某一时速的情况下,从开始制动到汽车完全静止时,车辆所开过的路程.制动距离越小,汽车的制动性能就越好.一般的道路制动距离 s(单位:m)与车辆速度 v(单位:km/h)之间的关系满足:$ s= av^{2}+bv $.现测得几组对应值如下表:
|v/(km/h)|20|30|40|50|60|70|…|
|s/m|2|4.5|8|12.5|18|24.5|…|

(1)写出制动距离 s 与车辆速度 v 之间的关系式.
(2)某一路段的限速为 60 km/h,如果一辆汽车超速 20%,则该汽车的制动距离将延长多少米?
(3)如图,一辆长为 4 m以 80 km/h 的速度匀速行驶 的小车行驶在路上,前方有一座桥,桥面宽 AC= 10 m.当车头外轮廓线距离桥侧面 CD 的距离为 n时,司机开始制动,车恰好停 在桥上(车头和车尾 的外轮廓线完全 在桥面上),求 n 的取值范围.|v/(km/h)|20|30|40|50|60|7|…|s/m|2|45|8|12|5|8|24|…|

|v/(km/h)|20|30|40|50|60|70|…|
|s/m|2|4.5|8|12.5|18|24.5|…|

(1)写出制动距离 s 与车辆速度 v 之间的关系式.
(2)某一路段的限速为 60 km/h,如果一辆汽车超速 20%,则该汽车的制动距离将延长多少米?
(3)如图,一辆长为 4 m以 80 km/h 的速度匀速行驶 的小车行驶在路上,前方有一座桥,桥面宽 AC= 10 m.当车头外轮廓线距离桥侧面 CD 的距离为 n时,司机开始制动,车恰好停 在桥上(车头和车尾 的外轮廓线完全 在桥面上),求 n 的取值范围.|v/(km/h)|20|30|40|50|60|7|…|s/m|2|45|8|12|5|8|24|…|

答案:
(1)将$ v=20,s=2;v=40,s=8 $代入$ s=av^{2}+bv $,得$ \begin{cases} 400a+20b=2, \\ 1600a+40b=8, \end{cases} $解得$ a=\frac{1}{200},b=0 $,
∴制动距离s与车辆速度v之间的关系式为$ s=\frac{1}{200}v^{2} $.
(2)
∵$ 60×(1+20\%)=72 $,
∴当$ v=72 $时,$ s=25.92 $,
∴25.92-18=7.92(米),
∴汽车的制动距离将延长7.92米.
(3)由题意,得$ n-6≤\frac{1}{200}×80^{2}≤n $,解得32≤n≤38,故n的取值范围为32≤n≤38.
(1)将$ v=20,s=2;v=40,s=8 $代入$ s=av^{2}+bv $,得$ \begin{cases} 400a+20b=2, \\ 1600a+40b=8, \end{cases} $解得$ a=\frac{1}{200},b=0 $,
∴制动距离s与车辆速度v之间的关系式为$ s=\frac{1}{200}v^{2} $.
(2)
∵$ 60×(1+20\%)=72 $,
∴当$ v=72 $时,$ s=25.92 $,
∴25.92-18=7.92(米),
∴汽车的制动距离将延长7.92米.
(3)由题意,得$ n-6≤\frac{1}{200}×80^{2}≤n $,解得32≤n≤38,故n的取值范围为32≤n≤38.
查看更多完整答案,请扫码查看


