《2025年实验班提优训练九年级数学上册浙教版》

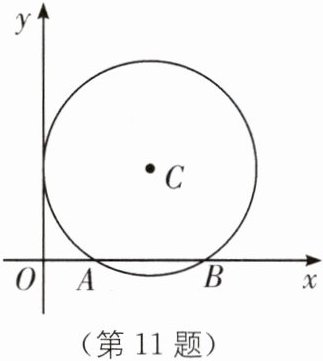
11. 如图,在平面直角坐标系中,以点$C(2,\sqrt{3})$为圆心,以2为半径的圆与$x轴交于A$,$B$两点.
(1)求$A$,$B$两点的坐标；
(2)若二次函数$y= x^{2}+bx+c的图象经过点A$,$B$,试确定此二次函数的表达式.

答案：
11.
(1)如图,过点C作CM⊥x轴于点M,连结AC,

则MA=MB,
∵点C的坐标为(2,√3),
∴OM=2,CM=√3.
在Rt△ACM中,CA=2,
∴AM=√(AC²−CM²)=1.
∴OA=OM−AM=1,OB=OM+BM=3.
∴点A的坐标为(1,0),点B的坐标为(3,0).
(2)将A(1,0),B(3,0)代入y=x²+bx+c,
得{1+b+c=0,9+3b+c=0,解得{b=-4,c=3.
∴二次函数的表达式为y=x²−4x+3.

12.(2025·江西上饶期中)如图,$OA= OB$,$AB交\odot O于点C$,$D$,$OE$是的半径,且$OE\perp AB于点F$.
(1)求证:$AC= BD$；
(2)若$CD= 6$,$EF= 1$,求$\odot O$的半径.

答案：
12.
(1)
∵OE⊥AB,CD为⊙O的弦，
∴CF=DF.
∵OA=OB,OE⊥AB,
∴AF=BF,
∴AF−CF=BF−DF,
∴AC=BD,
(2)如图，连结OC,

∵OE⊥AB,CD为⊙O的弦，
∴CF=1/2CD=3,∠OFC=90°,
∴CO²=CF²+OF²,
设⊙O的半径是r,
∴r²=3²+(r−1)²,
解得r=5,
∴⊙O的半径是5.

13. 传统文化 圆形拱门屏风 圆形拱门屏风是中国古代家庭中常见装饰隔断,既美观又实用,彰显出中国元素的韵味如图是一款拱门示意图,其中C为AB中点,D为拱门最高点,线段CD经过圆心 O,已知拱门的半径为1.5m,拱门最下端AB= 1.8m.
(1)求拱门最高点D到地面的距离;
(2)现需要给房间内搬进一个长 和宽为2m,高为1.2m的桌子,已知搬桌子的两名工人在搬运时所抬高高度相同,且高度为0.5m,判断搬运该桌子时是否能够通过拱门.(参考数据:$\sqrt{5}\approx 2.236$)

答案：
13.
(1)如图
(1)中,连结AO.
∵CD⊥AB,CD经过圆心O,
∴AC=CB=0.9m,
∴OC=√(AO²−AC²)=√(1.5²−0.9²)=1.2(m),
∴CD=OD+OC=1.5+1.2=2.7(m),
∴拱门最高点D到地面的距离为2.7m.
(2)如图
(2),弦EF=2m,且EF⊥CD,垂足为J,连结OE.
∵C为AB中点,CD经过圆心,
∴EJ=JF=1m,CD⊥AB,
∴OJ=√(OE²−EJ²)=√(1.5²−1²)=√5/2≈1.118,
∴CJ=1.2-1.118=0.082(m).
∵0.5＞0.082,2OJ+CJ＞1.2+0.5=1.7(m),
∴搬运该桌子时能够通过拱门.

14.(2025·杭州西湖区期中)如图,$\odot O的直径AB垂直于弦CD$,垂足为$E$,$AE= 2$,$CD= 8$.
(1)求$\odot O$的半径长;
(2)连结$BC$,作$OF\perp BC于点F$,求$OF$的长.

答案：
14.
(1)连结OD,如图,设⊙O的半径长为r.

∵AB⊥CD,
∴∠OED=90°,DE=CE=1/2CD=1/2×8=4,
在Rt△ODE中,
∵OE=r-2,OD=r,DE=4,
∴(r-2)²+4²=r²,解得r=5,
即⊙O的半径长为5.
(2)在Rt△BCE中,
∵CE=4,BE=AB-AE=8,
∴BC=√(4²+8²)=4√5.
∵OF⊥BC,
∴BF=CF=1/2BC=2√5,∠OFB=90°,
在Rt△OBF中,OF=√(OB²−BF²)=√(5²-(2√5)²)=√5,即OF的长为√5.