《2025年实验班提优训练九年级数学上册浙教版》

9. 隐圆模型 如图,点A,B的坐标分别为$A(6,0)$,$B(0,8)$,点C为坐标平面内一点,$BC= 1$,点M为线段AC的中点,连结OM,则OM的最大值为______.

答案：
$\frac{11}{2}$ [解析]如图，
∵点C为坐标平面内一点，BC=1，
∴点C在以B为圆心的半径为1的圆上.
取OD=OA=6，连结CD.
∵AM=CM，OD=OA，

∴OM是△ACD的中位线，
∴OM=$\frac{1}{2}$CD.
当OM最大时，即CD最大，此时当D,B,C三点共线，且C在DB的延长线上时，OM最大.
∵OB=8，OD=6，∠BOD=90°，
∴BD=10，
∴CD=11，
∴OM=$\frac{1}{2}$CD=$\frac{11}{2}$，即OM的最大值为$\frac{11}{2}$.

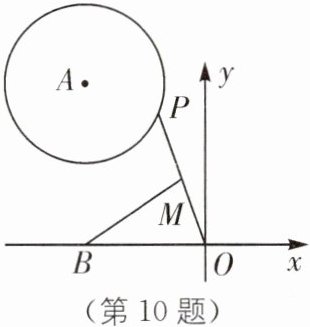
10. 中考新考法 最值问题 如图,在平面直角坐标系中,点$A(-6,8)$,$B(-6,0)$,以点A为圆心,4为半径作$\odot A$,点P为$\odot A$上一动点,M为OP的中点,连结BM,设BM的最大值为m,最小值为n,则$m-n$的值为______.

答案：
4 [解析]如图，在x轴上取一点E(−12,0)，连结PE,AE,AB,AE交⊙A于点P''，EA的延长线交⊙A于点P'.

∵B(−6,0)，A(−6,8)，
∴OB=BE=6，AB=8，AB⊥x轴，
∴∠ABE=90°，
∴AE=$\sqrt{AB^{2}+BE^{2}}$=10.
∵OM=PM，OB=BE，
∴BM=$\frac{1}{2}$PE.
∵点P在⊙A上运动，
∴当P,A,E共线时，EP可以取得最大值或最小值，最大值为EP'=10+4=14，最小值为EP''=10-4=6，
∴BM的最大值为$\frac{1}{2}$EP'=7，最小值为$\frac{1}{2}$EP''=3，
∴m=7，n=3，
∴m-n=4.

11. 新情境 降低沙尘暴影响 (2024·山东临沂期中)由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴的侵袭. 近日,A城气象局测得沙尘暴中心在A市的正西方向距A市240 km的B处,以每小时12 km的速度向北偏东$60^\circ$方向移动,如图所示,已知距沙尘暴中心150 km的范围为受影响区域.
(1)A城是否受这次沙尘暴的影响？为什么？
(2)若A城受这次沙尘暴的影响,则遭受影响的时间有多长？

答案：

(1)A城受这次沙尘暴的影响.理由如下：
如图，过点A作AC⊥BM，垂足为C，
在Rt△ABC中，由题意可知∠CBA=30°，
∴AC=$\frac{1}{2}$AB=$\frac{1}{2}$×240=120(km).
∵120＜150，
∴A城将受这次沙尘暴的影响.
(2)如图，设点E,F是以A为圆心，150km为半径的圆与MB的交点，连结AE,AF.

由题意，得CE=$\sqrt{AE^{2}-AC^{2}}$=90km，
∴EF=2CE=2×90=180(km)，
∴A城受沙尘暴影响的时间为180÷12=15(小时).
故A城将受到这次沙尘暴的影响，影响的时间为15小时.

12. 数形结合思想 如图$\odot M$的半径为2,圆心M的坐标为$(3,4)$,点P是$\odot M$上任意一点,$PA\perp PB$,且PA,PB与x轴分别交于A,B两点,若点A,B关于原点O对称,求AB的最小值.

答案：
如图，连结OP.
∵PA⊥PB，
∴∠APB=90°.
∵AO=BO，
∴AB=2PO.
若要使AB取得最小值，则PO需取得最小值，连结OM，交⊙M于点P'，当点P位于点P'位置时，OP'取得最小值，过点M作MQ⊥x轴于点Q，如图，

则OQ=3，MQ=4，
∴OM=5.
又MP'=2，
∴OP'=3，
∴AB=2OP'=6.
即AB的最小值为6.

13. 如图,在$\triangle ABC$中,$AB= AC= 2\sqrt{5}$,$BC= 4$,点D是AB的中点,若以点D为圆心,r为半径作$\odot D$,使点B在$\odot D$内,点C在$\odot D$外,试求r的取值范围.

精题详解

答案：
如图，连结CD，过点A作AE⊥BC于点E.过点D作DF⊥BC于点F，显然DF//AE.

CD不是直角三角形的一边，则要构造直角三角形来求线段CD的长度
∵AB=AC=2$\sqrt{5}$，BC=4，
根据AB=AC，联想到等腰三角形“三线合一”，结合勾股定理可求出高AE的长度
∴BE=$\frac{1}{2}$BC=2，
∴AE=$\sqrt{AB^{2}-BE^{2}}$=4.
∵点D是AB的中点，
∴DF是△ABE的中位线，
∴DF=$\frac{1}{2}$AE=2，BF=$\frac{1}{2}$BE=1，
∴CF=3，
∴CD=$\sqrt{DF^{2}+CF^{2}}$=$\sqrt{13}$.
又DB=$\frac{1}{2}$AB=$\sqrt{5}$，
∴r的取值范围是$\sqrt{5}$＜r＜$\sqrt{13}$.