《2025年实验班提优训练九年级数学上册浙教版》

1.（2024·宁波镇海区期末）若一个扇形的半径是4,圆心角为90°,则此扇形的面积为（C）.
A.π
B.2π
C.4π
D.8π

答案： C [解析]
∵扇形的半径是4，圆心角为90°，
∴扇形面积为$\frac{90\pi×4^{2}}{360}=4\pi$。知识拓展　扇形面积计算公式：设圆心角是$n^{\circ}$，圆的半径为R的扇形面积为S，则$S_{扇形}=\frac{n\pi R^{2}}{360}$或$S_{扇形}=\frac{1}{2}lR$（其中l为扇形的弧长）。

2. 实验班原创 在$\odot O$中,若扇形的弧长为$6\pi$,半径为6,则扇形的面积是______18π.

答案： 18π

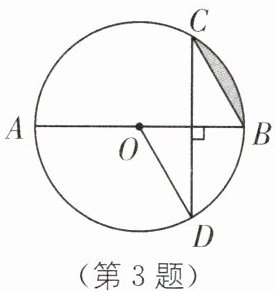
3. 如图,AB是$\odot O$的直径,CD为弦,$AB\perp CD$,若$CD=2\sqrt{3}$,$CB=2$,则阴影部分的面积是______$\frac{2\pi}{3}-\sqrt{3}$.

答案： $\frac{2\pi}{3}-\sqrt{3}$ [解析]如图，连结OC，设CD与AB的交点为E。
∵AB是$\odot O$的直径，$AB\perp CD$，$CD=2\sqrt{3}$，$CB=2$，
∴$CE=\sqrt{3}$，
∴$BE=\sqrt{2^{2}-(\sqrt{3})^{2}}=1$，
∴$\angle ECB=30^{\circ}$，$\angle CBE=60^{\circ}$。
∵$CO=BO$，
∴$\triangle OBC$是等边三角形，
∴$\angle BOC=60^{\circ}$，$OC=CB=2$，
∴$S_{阴影}=\frac{60\pi×2^{2}}{360}-\frac{1}{2}×2×\sqrt{3}=\frac{2\pi}{3}-\sqrt{3}$。归纳总结　不规则图形面积的求法：将不规则图形转化为几个规则图形的面积再求解，如本题将弓形转化为扇形与三角形，将两个图形面积相减即可。

4. 实验班原创 如图,某玩具品牌的标志由半径为6 cm 的三个等圆构成,且三个等圆$\odot O_{1}$,$\odot O_{2}$,$\odot O_{3}$相互经过彼此的圆心,则图中三个阴影部分的面积之和为______.

$18\pi\ cm^{2}$

答案： $18\pi\ cm^{2}$ [解析]如图，连结$O_{1}A$，$O_{2}A$，$O_{1}B$，$O_{3}B$，$O_{2}C$，$O_{3}C$，$O_{1}O_{2}$，$O_{1}O_{3}$，$O_{2}O_{3}$，则$\triangle O_{1}AO_{2}$，$\triangle O_{1}BO_{3}$，$\triangle O_{2}CO_{3}$，$\triangle O_{1}O_{2}O_{3}$都是边长为1的正三角形，所以$S_{阴影部分}=3S_{扇形AO_{1}O_{2}}=3×\frac{60\pi×6^{2}}{360}=18\pi(\ cm^{2})$。

5. 新情境 杭州亚运会 （2024·宁波鄞州区期末）如图（1）是杭州第19届亚运会会徽"潮涌",其主体为图（2）中的扇环.延长CA,DB交于点O,$\angle AOB=120^\circ$,若$AB=5\sqrt{3}\ \text{cm}$,$AC=4\ \text{cm}$,则图（2）中扇环的面积为______$\text{cm}^2$（结果保留π）.

$\frac{56}{3}\pi$

答案： $\frac{56}{3}\pi$ [解析]如图，作$OE\perp AB$于点E。
∵$OA=OB$，$\angle AOB=120^{\circ}$，$AB=5\sqrt{3}\ cm$，
∴$AE=\frac{5\sqrt{3}}{2}\ cm$，$\angle AOE=60^{\circ}$，
∴$\angle OAE=30^{\circ}$，
∴$OE=\frac{1}{2}OA$。在$\text{Rt}\triangle AOE$中，由勾股定理，得$OA^{2}=OE^{2}+AE^{2}$，
∴$OA^{2}=(\frac{1}{2}OA)^{2}+(\frac{5\sqrt{3}}{2})^{2}$，
∴$OA=5\ cm$（负值已舍去），
∴$OC=5+4=9(\ cm)$，
∴扇环的面积为$\frac{120\pi×9^{2}}{360}-\frac{120\pi×5^{2}}{360}=\frac{56}{3}\pi(\ cm^{2})$。

6. 某停车场入口的栏杆如图所示,栏杆从水平位置AB绕点O旋转到$A'B'$的位置,已知$AO=3\ \text{m}$,若栏杆的旋转角$\angle AOA'=40^\circ$,则AO部分扫过的图形的面积为（D）.

A.$\frac{\pi}{3}\ \text{m}^2$
B.$\frac{2\pi}{3}\ \text{m}^2$
C.$2\pi\ \text{m}^2$
D.$\pi\ \text{m}^2$

]

答案： D [解析]
∵$R=3\ m$，$\angle AOA'=40^{\circ}$，
∴$S=\frac{n\pi R^{2}}{360}=\frac{40\pi×3^{2}}{360}=\pi(\ m^{2})$。故选D。

7. 传统文化 纸扇 （2024·东营中考）习近平总书记强调,中华优秀传统文化是中华民族的根和魂.东营市某学校组织开展中华优秀传统文化成果展示活动,小慧同学制作了一把扇形纸扇.如图,$OA=20\ \text{cm}$,$OB=5\ \text{cm}$,纸扇完全打开后,外侧两竹条（竹条宽度忽略不计）的夹角$\angle AOC=120^\circ$,现需在扇面一侧绘制山水画,则山水画所在纸面的面积为（C）$\text{cm}^2$.
A.$\frac{25\pi}{3}$
B.$75\pi$
C.$125\pi$
D.$150\pi$

答案： C [解析]由题知，$S_{扇形OAC}=\frac{120\pi×20^{2}}{360}=\frac{400}{3}\pi(\ cm^{2})$，$S_{扇形OBD}=\frac{120\pi×5^{2}}{360}=\frac{25}{3}\pi(\ cm^{2})$，所以山水画所在纸面的面积为$\frac{400}{3}\pi-\frac{25}{3}\pi=125\pi(\ cm^{2})$。故选C。

8. 如图,菱形ABCD的对角线AC,BD相交于点O,$AC=8$,$BD=6$,以AB为直径作一个半圆,则图中阴影部分的面积为（D）.
A.$25\pi-6$
B.$\frac{25\pi}{2}-6$
C.$\frac{25\pi}{6}-6$
D.$\frac{25\pi}{8}-6$

]

答案： D [解析]由菱形的性质，易知$AO=4$，$BO=3$，$\angle AOB=90^{\circ}$。在$\text{Rt}\triangle ABO$中，$AB=\sqrt{AO^{2}+BO^{2}}=5$，
∴以AB为直径的半圆面积为$\frac{1}{2}\pi×(\frac{5}{2})^{2}=\frac{25}{8}\pi$，
∴$S_{阴影}=S_{半圆}-S_{\triangle AOB}=\frac{25}{8}\pi-\frac{1}{2}×4×3=\frac{25\pi}{8}-6$。故选D。

9. 如图,AB为半圆的直径,且$AB=4$,半圆绕点B顺时针旋转$45^\circ$,点A旋转到$A'$的位置,则图中阴影部分的面积为（B）.
A.π
B.2π
C.$\frac{\pi}{2}$
D.4π

答案： B [解析]$S_{阴影}=S_{扇形BAA'}+S_{半圆}-S_{半圆}=S_{扇形BAA'}=\frac{45\pi×4^{2}}{360}=2\pi$。故选B。