《2025年实验班提优训练九年级数学上册浙教版》

8. (2025·辽宁大连沙河口区期中)一个水杯竖直放置时的纵向截面如图(1)所示,其左右轮廓线 AC,BD 都是同一条抛物线的一部分,AB,CD 都与水面桌面平行,已知水杯底部 AB 宽为 4√3 cm,水杯高度为 12 cm,当水面高度为 6 cm 时,水面宽度为 2√30 cm. 如图(2)先把水杯盛满水,再将水杯绕 A 点倾斜倒出部分水,如图(3),当倾斜角∠BAF= 30°时,杯中水面 CE 平行水平桌面 AF,则此时水面 CE 的值是( D ).
A.7√3 cm
B.12 cm
C.8√3 cm
D.14 cm

答案： D　[解析]如图
(1),以AB的中点为原点，直线AB为x轴，线段AB的中垂线为y轴，建立平面直角坐标系.由题意，得A(−2$\sqrt{3}$,0),B(2$\sqrt{3}$,0),M(−$\sqrt{30}$,6),N($\sqrt{30}$,6).设抛物线对应的函数表达式为y=ax²+b.将B(2$\sqrt{3}$,0),N($\sqrt{30}$,6)代入，得$\left\{\begin{array}{l} 12a+b=0,\\ 30a+b=6\end{array}\right. $解得$\left\{\begin{array}{l} a=\frac{1}{3},\\ b=-4,\end{array}\right. $
∴y=$\frac{1}{3}$x²−4.当y=12时,12=$\frac{1}{3}$x²−4,解得x₁=4$\sqrt{3}$,x₂=−4$\sqrt{3}$,
∴C(−4$\sqrt{3}$,12),D(4$\sqrt{3}$,12).根据题意可知,∠DCE=∠BAF=30°,如图
(2),设CE与y轴交于点P,CD与y轴交于点Q.在Rt△CPQ中,
∵CQ=4$\sqrt{3}$cm,∠PCQ=30°,
∴PQ=4cm,
∴PO=8cm,
∴P(0,8).设直线CE的表达式为y=kx+m,将C(−4$\sqrt{3}$,12),P(0,8)代入，得$\left\{\begin{array}{l} -4\sqrt{3}k+m=12,\\ m=8,\end{array}\right. $解得$\left\{\begin{array}{l} k=-\frac{\sqrt{3}}{3},\\ m=8,\end{array}\right. $
∴直线CE的表达式为y=−$\frac{\sqrt{3}}{3}$x+8.令$\frac{1}{3}$x²−4=−$\frac{\sqrt{3}}{3}$x+8,解得x=−4$\sqrt{3}$或x=3$\sqrt{3}$
∴点E的横坐标为3$\sqrt{3}$当x=3$\sqrt{3}$时,y=−$\frac{\sqrt{3}}{3}$×3$\sqrt{3}$+8=5,
∴E(3$\sqrt{3}$,5).
∴CE=$\sqrt{(3\sqrt{3}+4\sqrt{3})^{2}+(5-12)^{2}}$=14(cm).故选D.

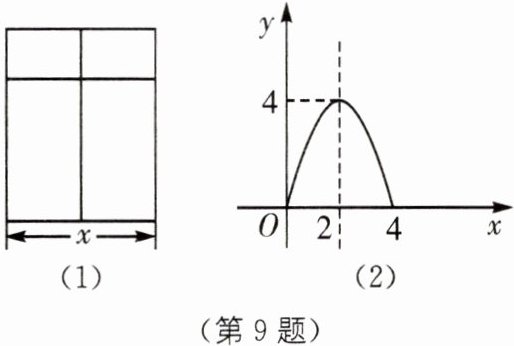
9. 实验班原创 用总长为 a 米的材料做成如图(1)所示的矩形窗框,设窗框的宽为 x 米,窗框的透光面积为 y 平方米,y 关于 x 的函数图象如图(2)所示,则$ a^2 $的值是______.

144

答案： 144　[解析]由图象可知,当x=2时,y最大=4,
∴当x=2时，窗框的最大透光面积是4平方米，
∴矩形窗框的另一边长为4÷2=2(米),
∴a=3×2+3×2=12,
∴a²=144.方法诠释　本题考查了二次函数的应用,从图象中获取相关信息解决问题是学习函数的基本功，体现了数形结合的思想方法

10. (2024·泰安中考)如图,小明的父亲想用长为 60 米的栅栏,再借助房屋的外墙围成一个矩形的菜园. 已知房屋外墙长 40 米,则可围成的菜园的最大面积是450平方米.

答案： 450　[解析]由题意，设垂直于墙的边长为x米，则平行于墙的边长为(60−2x)米.
∵房屋外墙长为40米，
∴0＜60−2x≤40,
∴10≤x＜30.菜园的面积=x(60-2x)=−2x²+60x=−2(x−15)²+450,
∴当x=15时,可围成的菜园的最大面积是450,即垂直于墙的边长为15米时，可围成的菜园的最大面积是450平方米.

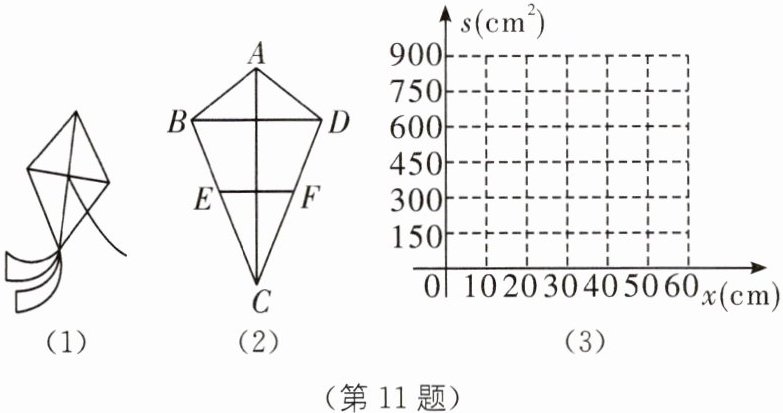
11. (2025·宁波鄞州区期末)如图(1)所示风筝的筝面可以抽象成图(2)的筝形 ABCD,AB= AD,CB= CD,风筝的骨架由 3 条竹棒 AC,BD,EF 组成,其中 E,F 分别是 CB 和 CD 的中点. 现有一根总长为 90 cm 的竹棒可截成三段做风筝的骨架. 为合理利用筝面 ABCD 的材料,作了如下探究：
(1)设筝面 ABCD 的面积为$ s(cm^2),$骨架 BD 的长度为 x(cm),求 s 关于 x 的函数关系式；
(2)在图(3)中画出(1)中 s 关于 x 的函数图象；
(3)利用图象分析,当骨架 AC 长度大于 BD 长度且筝面的面积超过$ 432 cm^2 $时,骨架 BD 的长度范围.

答案：
(1)
∵AB=AD,CB=CD,
∴AC是BD的垂直平分线.
∵E,F分别是CB和CD的中点,
∴EF=$\frac{1}{2}$BD.
∴s=$\frac{1}{2}$AC·BD=$\frac{1}{2}$(90−$\frac{3}{2}$x)x=−$\frac{3}{4}$x²+45x(0＜x＜60).
(2)s=−$\frac{3}{4}$x²+45x=−$\frac{3}{4}$(x−30)²+675(0＜x＜60),
∴当x=30时,s取最大值675.当y=0时,得−$\frac{3}{4}$(x−30)²+675=0,解得x₁=0,x₂=60,
∴s关于x的函数图象如图所示.
(3)当s=432时,−$\frac{3}{4}$x²+45x=432,解得x=12或48,由AC＞BD得,90−$\frac{3}{2}$x＞x,解得x＜36,
∴当12＜BD＜36时，筝面的面积超过432cm².