《2025年实验班提优训练九年级数学上册浙教版》

10. 如图,小方格都是边长为1的正方形,则以格点为圆心,半径分别为1和2的两种弧围成的"叶状"阴影图案的面积为（B）.
A.$\pi-2$
B.$2\pi-4$
C.$4\pi-4$
D.$8\pi-8$

]

答案： B [解析]如图，连结AB，BC。$S_{阴影}=2×(S_{扇形OAB}-S_{\triangle AOB})=2×(\frac{90\pi×2^{2}}{360}-\frac{1}{2}×2^{2})=2\pi-4$。

11. （2024·自贡二模）如图,在$\triangle ABC$中,$\angle ABC=90^\circ$,$\angle ACB=30^\circ$,$AB=4$,点O为BC 的中点,以O为圆心,OB长为半径作半圆,交AC于点D,则图中阴影部分的面积是______.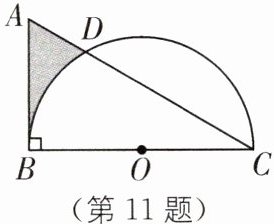
]
$5\sqrt{3}-2\pi$

答案： $5\sqrt{3}-2\pi$ [解析]如图，连结OD，过点D作$DE\perp BC$于点E。在$\triangle ABC$中，$\angle ABC=90^{\circ}$，$\angle ACB=30^{\circ}$，$AB=4$，
∴$AC=8$，
∴$BC=\sqrt{AC^{2}-AB^{2}}=4\sqrt{3}$，
∴$OC=OD=OB=2\sqrt{3}$。
∵$\angle DOB=2\angle C=60^{\circ}$，
∴$\angle ODE=30^{\circ}$，$DE=3$。
∴$S_{阴影}=S_{\triangle ACB}-S_{\triangle COD}-S_{扇形DBO}=\frac{1}{2}×4×4\sqrt{3}-\frac{1}{2}×2\sqrt{3}×3-\frac{60\pi×(2\sqrt{3})^{2}}{360}=5\sqrt{3}-2\pi$。

12. 如图,分别以点A,C为圆心,AD,CB的长为半径画弧,两弧相交于B,D两点.若$AB=2$,$\angle BAD=60^\circ$,则图中阴影部分的面积为$\frac{4\pi}{3}-2\sqrt{3}$.

答案： $\frac{4\pi}{3}-2\sqrt{3}$ [解析]连结BD。
∵四边形ABCD是菱形，
∴$AB=BC=CD=AD=2$，$\angle BAD=\angle BCD=60^{\circ}$，
∴$\triangle ABD$，$\triangle BDC$都是等边三角形，
∴$S_{阴}=S_{扇形ADB}+S_{扇形CDB}-S_{菱形ABCD}=2×\frac{60\pi×2^{2}}{360}-2×\frac{\sqrt{3}}{4}×2^{2}=\frac{4\pi}{3}-2\sqrt{3}$

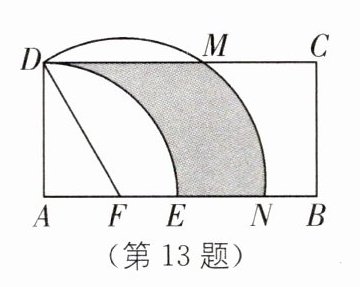
13.(2025·宁波镇海区月考)如图,在矩形ABCD 中，AD=√3,F是AB上一点,AF=1,以点A为圆心,AD为半径画弧,交AB于点E,以F为圆心,DF为半径画弧,交CD于点M,交AB于点N,则阴影部分的面积为___.

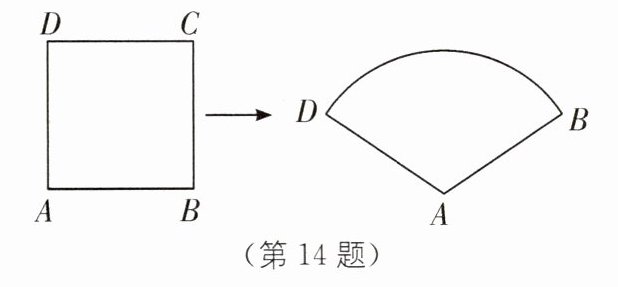
14.将如图所示的边长为1的正方形铁丝框变形成以A为圆心,AB为半径的扇形(铁丝的粗细忽略不计),则所得扇形DAB的面积是______

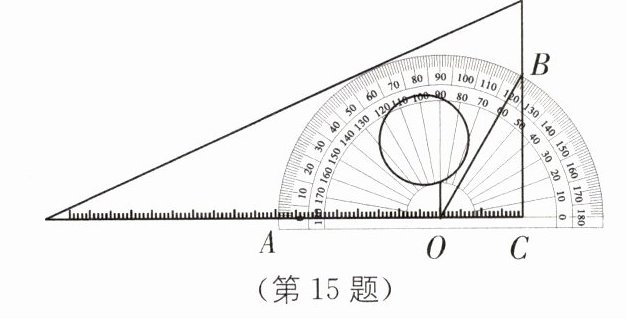
15.如图,将一块三角板和半圆形量角器按图中方式叠放,三角板一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧AB对应的圆心角∠AOB为120°,OC的长为2 cm,求三角板和量角器重叠部分的面积.

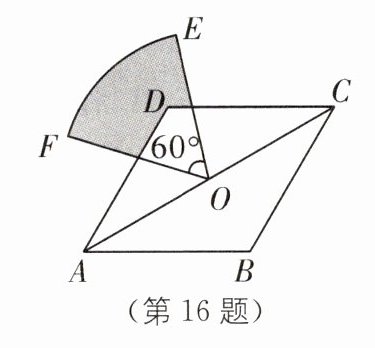
16.(2024·日照中考改编)如图,在菱形ABCD中，AB=2,∠B=120°,点0是对角线AC的中点,以点O为圆心,OA长为半径作圆心角为60°的扇形OEF,点D在扇形OEF内,求图中阴影部分的面积.

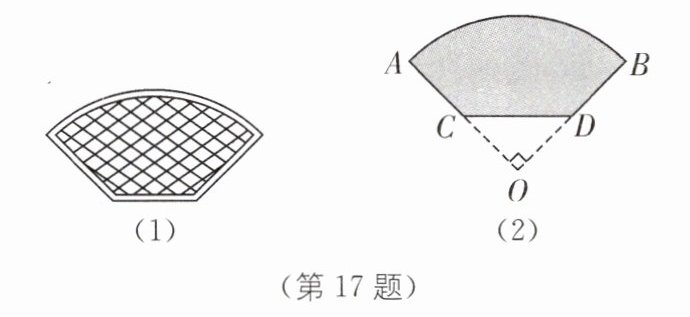
17.(2024·山西中考改编)如图(1)是小区围墙上的花窗,其形状是扇形的一部分,图(2)是其几何示意图(阴影部分为花窗).通过测量得到扇形AOB的圆心角为90°,OA=1 m,点C,D分别为OA,OB的中点,求花窗的面积.

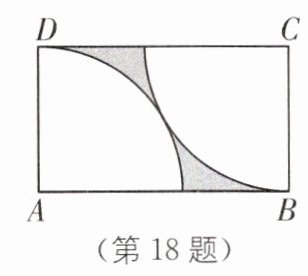
18.(2024·重庆中考改编)如图,在矩形ABCD 中,分别以点A和C为圆心,AD长为半径画弧，两弧有且仅有一个公共点.若AD=4,求图中阴影部分的面积.

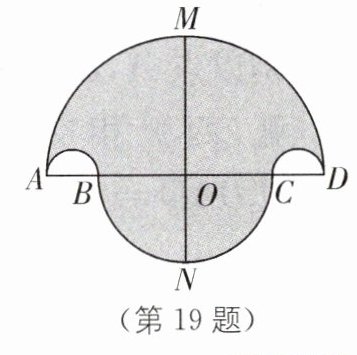
19.转化思想如图,已知B,C是线段AD上的两点,且AB=CD,分别以AB,BC,CD,AD为直径画四个半圆,得到一个如图所示的轴对称图形.此图的对称轴分别交其中两个半圆于点M,N,交AD 于点O.若AD=16,AB=2r(0<r<4),回答下列问题:

(1)用含r的代数式表示BC=__

MN=_______;

(2)设以MN为直径的圆的面积为S,阴影部分的面积为S阴影,请通过计算填写下表:

(3)由此表猜想S与S阴影的大小关系，并证明你的猜想。

答案： 13.$\frac{3\sqrt{3}}{2}-\frac{\pi}{12}$
14.1 [解析]
∵$l_{\overset{\frown}{BD}}=CD+BC=1+1=2$,
∴$S_{扇形ABD}=\frac{1}{2}l_{\overset{\frown}{BD}}\cdot AB=\frac{1}{2}\times2\times1=1$.
15.
∵$\angle AOB=120^{\circ}$,
∴$\angle BOC=60^{\circ}$.
∵$\angle C=90^{\circ}$,
∴$\angle OBC=30^{\circ}$. 在$\text{Rt}\triangle OBC$中,$OC=2\ \text{cm}$,$\angle OBC=30^{\circ}$,
∴$OB=4\ \text{cm}$,
∴$BC=2\sqrt{3}\ \text{cm}$.
∴$S_{扇形OAB}=\frac{120\pi\times4^{2}}{360}=\frac{16\pi}{3}(\text{cm}^{2})$, $S_{\triangle OBC}=\frac{1}{2}OC\cdot BC=2\sqrt{3}\ \text{cm}^{2}$. 故$S_{重叠部分}=S_{扇形OAB}+S_{\triangle OBC}=(\frac{16\pi}{3}+2\sqrt{3})\ \text{cm}^{2}$.
16.如图,过O作$ON\perp AD$,$OM\perp CD$,连结OD. （第16题）
∵$\angle ADC+\angle HOG=180^{\circ}$,
∴$\angle NHO+\angle DGO=180^{\circ}$.
∵$\angle DGO+\angle MGO=180^{\circ}$,
∴$\angle NHO=\angle MGO$.
∵四边形ABCD为菱形,
∴DO平分$\angle ADC$,
∴$OM=ON$. 在$\triangle ONH$和$\triangle OMG$中,$\begin{cases} \angle NHO=\angle MGO, \\ \angle ONH=\angle OMG, \\ ON=OM, \end{cases}$
∴$\triangle ONH\cong\triangle OMG(\text{AAS})$,
∴$\triangle ONH$的面积=$\triangle OMG$的面积,
∴四边形HOGD的面积=四边形NOMD的面积=$2\triangle OMD$的面积.
∵$\angle ODC=60^{\circ}$,
∴$\angle OCD=30^{\circ}$,
∴$OD=\frac{1}{2}CD=1$,
∴$OC=\sqrt{3}$.
∴$DM=\frac{1}{2}OD=\frac{1}{2}$,
∴$OM=\frac{\sqrt{3}}{2}$,
∴四边形HOGD的面积=$2\triangle OMD$的面积=$2\times\frac{1}{2}\times\frac{1}{2}\times\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{4}$,
∴阴影部分的面积=扇形的面积-四边形HOGD的面积=$\frac{60\pi\times(\sqrt{3})^{2}}{360}-\frac{\sqrt{3}}{4}=\frac{\pi}{2}-\frac{\sqrt{3}}{4}$.
17.由题知,$S_{扇形OAB}=\frac{\pi}{4}\ \text{m}^{2}$.
∵点C,D分别是OA,OB的中点,
∴$OC=OD=\frac{1}{2}\ \text{m}$,
∴$S_{\triangle OCD}=\frac{1}{2}\times\frac{1}{2}\times\frac{1}{2}=\frac{1}{8}(\text{m}^{2})$,
∴花窗的面积为$(\frac{\pi}{4}-\frac{1}{8})\ \text{m}^{2}$.
 18.连结AC.
∵两弧有且仅有一个公共点,$AD=4$,
∴$AC=2AD=8$,
∴在$\text{Rt}\triangle ADC$中, $CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{8^{2}-4^{2}}=4\sqrt{3}$,
∴$S_{矩形ABCD}=AD\cdot CD=16\sqrt{3}$.
∵两个扇形的圆心角均为$90^{\circ}$,且它们的半径均为4,
∴两个扇形面积之和为$S_{两个扇形}=\frac{180\pi AD^{2}}{360}=8\pi$,
∴$S_{阴影}=S_{矩形ABCD}-S_{两个扇形}=16\sqrt{3}-8\pi$.
19.
(1)$16-4r$ $16-2r$
(2)$49\pi$ $36\pi$ $25\pi$
(3)$S=S_{阴影}$.证明如下: $S=(\frac{16-2r}{2})^{2}\pi=(8-r)^{2}\pi=(64+r^{2}-16r)\pi$,$S_{阴影}=\frac{1}{2}\times(\frac{16}{2})^{2}\pi+\frac{1}{2}\times(\frac{16-4r}{2})^{2}\pi-\pi r^{2}=(r^{2}+64-16r)\pi$. 故$S=S_{阴影}$.