《2025年实验班提优训练九年级数学上册浙教版》

1. (1)如图(1)是一条线段,AB 的长为 10 cm, MN 的长为 2 cm,假设可以随意在这条线段上取一点,求这个点在线段 MN 上的概率;
(2)如图(2)是一个木制圆盘,图中是两个同心圆,其中大圆直径为 20 cm,小圆的直径为 10 cm,一只小鸟自由自在地在空中飞行,则小鸟停在小圆内(阴影部分)的概率是$\frac{1}{4}$.

答案： 1.
(1)因为 AB 的长为 10 cm,MN 的长为 2 cm,所以随意在这条线段上取一个点,这个点在线段 MN 上的概率为$\frac {2}{10}=\frac {1}{5}.$
(2)$\frac {1}{4}$[解析]由题意,得大圆的面积为$S_{1}=π(\frac {20}{2})^{2}=100π(cm^{2})$,小圆的面积为$S_{2}=π(\frac {10}{2})^{2}=25π(cm^{2})$.故小鸟停在小圆内(阴影部分)的概率是$\frac {25π}{100π}=\frac {1}{4}.$

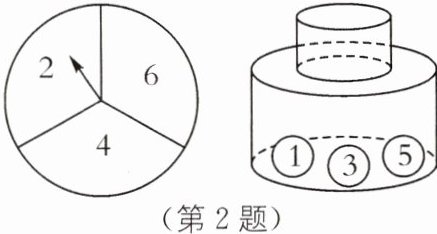
2. 有一个可自由转动的转盘,被分成了三个大小相同的扇形,分别标有数字 2,4,6;另有一个不透明的瓶子,装有分别标有数字 1,3,5 的三个完全相同的小球.小杰先转动一次转盘,停止后记下指针指向的数字(若指针指在分界线上则重转),小玉再从瓶子中随机取出一个小球,记下小球上的数字.
(1)请用列表或画树状图的方法(选其中一种)表示出所有可能出现的结果.
(2)若得到的两个数字之和是 3 的倍数,则小杰赢;若得到的两个数字之和是 7 的倍数,则小玉赢,此游戏公平吗?为什么?

答案： 2.
(1)用列表法表示所有可能出现的结果情况如下:
$\begin{array}{r} 2\quad4\quad6\\1\quad(2,1)\quad(4,1)\quad(6,1)\\3\quad(2,3)\quad(4,3)\quad(6,3)\\5\quad(2,5)\quad(4,5)\quad(6,5)\end{array}$
共有9种不同结果,即$(2,1),(2,3),(2,5),(4,1),(4,3),(4,5),(6,1),(6,3),(6,5).$
(2)公平.理由如下:列出得到的两个数字之和的所有可能的结果如下:
$\begin{array}{r} 2\quad4\quad6\\1\quad2+1=3\quad4+1=5\quad6+1=7\\3\quad2+3=5\quad4+3=7\quad6+3=9\\5\quad2+5=7\quad4+5=9\quad6+5=11\end{array}$
共有9种等可能的结果,其中"和为3的倍数"的结果有3种,"和为7的倍数"的结果有3种,
$\therefore P$(小杰胜)$=\frac {3}{9}=\frac {1}{3},P$(小玉胜)$=\frac {3}{9}=\frac {1}{3}.$
∴此游戏是公平的.
易错警示 本题考查列表法或画树状图法求等可能事件发生的概率,使用此方法一定注意每一种结果出现的可能性是均等的,即等可能事件.

3. 新情境 开展研学活动 (2024·宿迁中考)某校组织七年级学生开展以"讲好红色故事,传承红色基因"为主题的研学活动,策划了四条研学线路供学生选择:A 彭雪枫纪念馆,B 淮海军政大礼堂,C 爱园烈士陵园,D 大王庄党性教育基地,每名学生只能任意选择一条线路.
(1)小刚选择线路 A 的概率为______$\frac{1}{4}$;
(2)请用画树状图或列表的方法,求小刚和小红选择同一线路的概率.
列表如下:
$\begin{array}{r} A\quad B\quad C\quad D\\A\quad(A,A)\quad(A,B)\quad(A,C)\quad(A,D)\\B\quad(B,A)\quad(B,B)\quad(B,C)\quad(B,D)\\C\quad(C,A)\quad(C,B)\quad(C,C)\quad(C,D)\\D\quad(D,A)\quad(D,B)\quad(D,C)\quad(D,D)\end{array}$
共有16种等可能的结果,其中小刚和小红选择同一线路的结果有4种,
∴小刚和小红选择同一线路的概率为$\frac {4}{16}=\frac {1}{4}.$

答案： 3.
(1)$\frac {1}{4}$
(2)列表如下:
$\begin{array}{r} A\quad B\quad C\quad D\\A\quad(A,A)\quad(A,B)\quad(A,C)\quad(A,D)\\B\quad(B,A)\quad(B,B)\quad(B,C)\quad(B,D)\\C\quad(C,A)\quad(C,B)\quad(C,C)\quad(C,D)\\D\quad(D,A)\quad(D,B)\quad(D,C)\quad(D,D)\end{array}$
共有16种等可能的结果,其中小刚和小红选择同一线路的结果有4种,
∴小刚和小红选择同一线路的概率为$\frac {4}{16}=\frac {1}{4}.$