《2025年实验班提优训练九年级数学上册浙教版》

6. 某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
(1)若这个输水管道有水部分的水面宽$AB= 16\ \text{cm}$,水面最深地方的高度为4cm,求这个圆形截面的半径.
(2)在(1)的条件下,小明把一只宽12cm 的方形小木船放在修好后的圆柱形水管里,已知船高出水面13cm,问:此小船能顺利通过这个管道吗?

答案：
6.
(1)如图
(1)，设该圆形截面的圆心为O，过点O作OE⊥AB于点D，交弧AB于点E，连结OB.
　　　　　　　　
∵OE⊥AB，
∴BD=$\frac{1}{2}$AB=$\frac{1}{2}$×16=8(cm).
　由题意可知ED=4cm.
　设半径为xcm，则OD=(x−4)cm.
　在Rt△BOD中，由勾股定理，得OD²+BD²=OB²，
∴(x−4)²+8²=x²，解得x=10，
　即这个圆形截面的半径为10cm.
(2)小船能顺利通过这个管道.理由如下:
　　　　　　　
　如图
(2)，连结OM，由题意，得MN=12cm，EF⊥MN，
∴OM=10cm，MF=$\frac{1}{2}$MN=6cm，
∴在Rt△MOF中，OF= $\sqrt{OM^{2}-MF^{2}}$=8(cm)，
∴DF=OF+OD=8+(10−4)=14(cm).
∵14cm＞13cm，
∴小船能顺利通过这个管道.

7. 一题多问 如图,$\odot O$为等边三角形 ABC 的外接圆,半径为2,点 D 在劣弧$\overset{\frown}{AB}$上运动(不与点A,B 重合),连结 DA,DB,DC.
(1)求证:DC 是$\angle ADB$的平分线.
(2)四边形 ADBC 的面积 S 是线段 DC 的长x的函数吗? 如果是,求出函数表达式;如果不是,请说明理由.
(3)若点 M,N 分别在线段 CA,CB 上运动(不含端点),经过探究发现,点 D 运动到每一个确定的位置,$\triangle DMN$的周长有最小值t,随着点 D 的运动,t 的值会发生变化,求所有t值中的最大值.

答案：
7.
(1)
∵△ABC是等边三角形，
∴∠ABC=∠BAC=∠ACB=60°.
∵∠ADC=∠ABC=60°，∠BDC=∠BAC=60°，
∴∠ADC=∠BDC，
∴DC是∠ADB的平分线.
(2)四边形ADBC的面积S是线段DC的长x的函数，表达式为S=$\frac{\sqrt{3}}{4}$x²(2$\sqrt{3}$＜x≤4).理由如下:
　如图
(1)，将△ADC绕点C逆时针旋转60°，得到△BHC，
∴CD=CH，∠DAC=∠HBC.
∵四边形ACBD是圆内接四边形，
∴∠DAC+∠DBC=180°，
∴∠DBC+∠HBC=180°，
∴点D,B,H三点共线.
∵DC=CH，∠CDH=60°，
∴△DCH是等边三角形.
∵四边形ADBC的面积S=S△ADC+S△BDC=S△CDH=$\frac{\sqrt{3}}{4}$CD²，
∴S=$\frac{\sqrt{3}}{4}$x²(2$\sqrt{3}$＜x≤4).

(3)如图
(2)，作点D关于直线AC的对称点E，作点D关于直线BC的对称点F.
∵点D,E关于直线AC对称，
∴EM=DM.
　同理DN=NF.
∵C△DMN=DM+DN+MN=EM+FN+MN，
∴当点E,M,N,F四点共线时，△DMN的周长有最小值.连结EF，交AC于点M，交BC于点N，连结CD,CE,CF,DE,DF，过点C作CP⊥EF于点P，
∴C△DMN的最小值为EF=t.
∵点D,E关于直线AC对称，
∴CE=CD，∠ACE=∠ACD.
∵点D,F关于直线BC对称，
∴CF=CD，∠DCB=∠FCB，
∴CD=CE=CF，∠ECF=∠ACE+∠ACD+∠DCB+∠FCB=2∠ACB=120°.
∵CP⊥EF，CE=CF，∠ECF=120°，
∴EP=PF，∠CEP=30°，
∴PC=$\frac{1}{2}$EC，PE=$\frac{\sqrt{3}}{2}$EC，
∴EF=2PE=$\sqrt{3}$EC=$\sqrt{3}$CD=t，
∴当CD有最大值时，EF有最大值，即t有最大值.
∵CD为⊙O的弦，
∴CD为直径时，CD有最大值4，
∴t的最大值为4$\sqrt{3}$

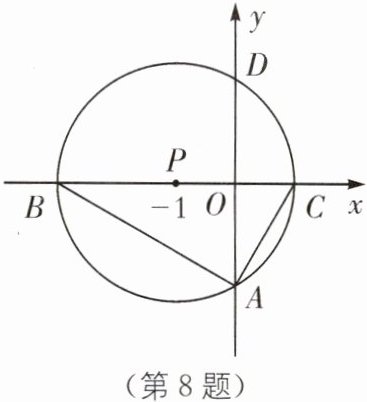
8. 一题多问 如图,以点$P(-1,0)$为圆心的圆,交x轴于 B,C 两点(B 在 C 的左侧),交 y 轴于A,D 两点(A 在 D 的下方),$AD= 2\sqrt{3}$,将$\triangle ABC$绕点 P 旋转$180^{\circ}$,得到$\triangle MCB$.
(1)求 B,C 两点的坐标.
(2)请在图中画出线段 MB,MC,并判断四边形ACMB 的形状(不必证明),求出点 M 的坐标.
(3)动直线 l 从与 BM 重合的位置开始绕点 B顺时针旋转,到与 BC 重合时停止.设直线 l与 CM 交点为 E,点 Q 为 BE 的中点,过点 E作$EG\perp BC$于G,连结 MQ,QG. 请问在旋转过程中$\angle MQG$的大小是否变化,若不变,求出$\angle MQG$的度数;若变化,请说明理由.

答案：
8.
(1)由垂径定理，得OA=$\frac{1}{2}$AD=$\sqrt{3}$.如图
(1)，连结PA，由勾股定理，得PA= $\sqrt{OA^{2}+OP^{2}}$= $\sqrt{3+1}$=2，
∴OB=OP+PB=1+2=3，OC=PC−OP=2−1=1，
∴B(−3,0)，C(1,0).
　
(2)如图
(2)，延长AP，交⊙P于点M，连结MB，MC，即为所要求画的线段.四边形ACMB是矩形.
　过点M作MN⊥x轴于点N，
∵∠MNP=∠AOP=90°，∠MPN=∠APO，PM=PA，
∴△MPN≌△APO，
∴MN=AO=$\sqrt{3}$，PN=PO=1，ON=2，
∴M(−2,$\sqrt{3}$).
(3)在旋转过程中∠MQG的大小不发生变化.
如图
(3)，在Rt△MBE和Rt△GBE中，
∵BQ=EQ，
∴MQ=QG=BQ，
∴∠BMQ=∠MBQ，∠QGB=∠QBG，
∴∠MQE=2∠MBQ，∠GQE=2∠GBQ，
∴∠MQG=2∠MBC.易知AC=AP=PC=2，
∴△PAC 为等边三角形，
∴∠PCA=60°，
∴∠MBC=60°，
∴∠MQG=2×60°=120°.