《2025年实验班提优训练九年级数学上册浙教版》

11. 网络销售已经成为一种热门的销售方式,为减少农产品的库存,某市市长亲自在某网络平台上进行直播销售某品牌板栗,为提高大家购买的积极性,直播时,板栗公司每天拿出 2000 元现金,作为红包发给购买者.已知该板栗的成本价格为 6 元/kg,每日销售量 y(kg)与销售单价 x(元/kg)满足关系式:$ y= -100x +5000 $.经销售发现,销售单价不低于成本价且不高于 30 元/kg .当每日销售量不低于 4000 kg时,每千克成本将降低1元,设板栗公司销售该板栗的日获利为 w(元).
(1)请求出日获利 w 与销售单价 x之间 的函数关系式.
(2)当销售单价定为多少时,销售这种板栗日获利最大?最大利润为多少元?
(3)当$ w\geq40000 $元时,网络平台将向板栗公司收取 a元/kg($ a＜4 $) 的相关费用,若此时日获利的最大值为 42100 元,求 a的值.

答案：
(1)当$ y≥4000 $,即$ -100x+5000≥4000 $时,$ x≤10 $.
∴当6≤x≤10时,$ w=(x-6+1)(-100x+5000)-2000=-100x^{2}+5500x-27000 $;当10＜x≤30时,$ w=(x-6)(-100x+5000)-2000=-100x^{2}+5600x-32000 $.综上所述,$ w=\begin{cases} -100x^{2}+5500x-27000(6≤x≤10), \\ -100x^{2}+5600x-32000(10＜x≤30). \end{cases} $
(2)当6≤x≤10时,$ w=-100x^{2}+5500x-27000=-100(x-\frac{55}{2})^{2}+48625 $.
∵a=-100＜0,对称轴为直线$ x=\frac{55}{2} $,
∴当6≤x≤10时,y随x的增大而增大,即当$ x=10 $时,$ w_{最大值}=18000 $;当10＜x≤30时,$ w=-100x^{2}+5600x-32000=-100(x-28)^{2}+46400 $.
∵a=-100＜0,对称轴为直线$ x=28 $,
∴当$ x=28 $时,$ w_{最大值}=46400 $.
∵46400＞18000,
∴当销售单价定为28元/kg时,销售这种板栗日获利最大,最大利润为46400元.
(3)
∵40000＞18000,
∴10＜x≤30,则$ w=-100x^{2}+5600x-32000 $.令$ w=40000 $,则$ 40000=-100x^{2}+5600x-32000 $,解得$ x_{1}=20,x_{2}=36 $,
∴当20≤x≤36时,$ w≥40000 $.又10＜x≤30,
∴20≤x≤30,此时日获利$ w_{1}=(x-6-a)(-100x+5000)-2000=-100x^{2}+(5600+100a)x-32000-5000a $,
∴对称轴为直线$ x=-\frac{5600+100a}{2×(-100)}=28+\frac{1}{2}a $.
∵a＜4,
∴$ 28+\frac{1}{2}a＜30 $,
∴当$ x=28+\frac{1}{2}a $时,$ w_{最大值}=42100 $.
∴$ (28+\frac{1}{2}a-6-a)[-100(28+\frac{1}{2}a)+5000]-2000=42100 $,解得$ a_{1}=2,a_{2}=86 $.
∵a＜4,
∴a=2.
归纳总结 解决最大利润问题时首先要理解题意,确定变量,建立函数模型,然后结合实际选择最优方案.解答时要注意自变量的取值范围,若顶点不在自变量的取值范围内,则利用函数的增减性来求最值.

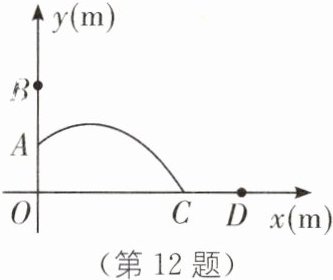
12. (2024·陕西中考)某广场的声控喷泉是由若干个垂直于地面的柱形喷泉装置组成的.每个柱形喷泉装置上都有上下两个喷头,这两个喷头朝向一致,喷出的水流均呈抛物线型.当围观游人喊声较小时,下喷头喷水;当围观游人喊声较大时,上下两个喷头都喷水.如图所示,点 A 和点 B 是一个柱形喷泉装置 OB 上的两个喷头,A 喷头喷出的水流的落地点为 C.以 O 为原点,以 OC 所在直线为 x 轴,OB 所在直线为 y 轴,建立平面直角坐标系.(柱形喷泉装置的粗细忽略不计)
已知:$ OA= 1m,OB= 2m,OC= 3m $,从 A 喷头和 B 喷头各喷出的水流的高度 y(m)与水平距离 x(m)之间的关系式分别是 $ y= -\frac{1}{3}x^{2}+bx+c $和 $ y= -\frac{1}{3}x^{2}+bx+c' $.
(1)求 A 喷头喷出的水流的最大高度.
(2)一名游人站在点 D 处,$ OD= 4m $.当围观游人喊声较大时,B 喷头喷出的水流是否会落在该游人所站的点 D 处?

答案：
(1)根据题意,令$ x=0 $,易得$ c=1,c'=2 $.令$ x=3,y=-\frac{1}{3}x^{2}+bx+c=-3+3b+1=0 $,可求得$ b=\frac{2}{3} $.因此A喷头和B喷头各喷出的水流的高度y(m)与水平距离x(m)之间的关系式分别是$ y=-\frac{1}{3}x^{2}+\frac{2}{3}x+1 $和$ y=-\frac{1}{3}x^{2}+\frac{2}{3}x+2 $.函数$ y=-\frac{1}{3}x^{2}+\frac{2}{3}x+1 $的对称轴为$ x=1 $,此时$ y=\frac{4}{3} $,因此A喷头喷出的水流的最大高度为$ \frac{4}{3} $m.
(2)函数$ y=-\frac{1}{3}x^{2}+\frac{2}{3}x+2 $,令$ x=4 $,$ y=-\frac{1}{3}×4^{2}+\frac{2}{3}×4+2=-\frac{2}{3} $,因此B喷头喷出的水流不会落在该游人所站的点D处.