《2025年实验班提优训练九年级数学上册浙教版》

1. (教材 P70 练习 T1·变式)小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为了到商店配到与原来大小一样的圆形玻璃,不能选择的应该是(B).

A.第①块
B.第②块
C.第③块
D.第④块

答案： 1.B　[解析]第①④块出现一段完整的弧，可在这段弧上任作两条弦，作出这两条弦的垂直平分线，两条垂直平分线的交点就是圆心，进而可得到半径的长；第③块有三点在圆上，作出这两条弦的垂直平分线，两条垂直平分线的交点就是圆心，进而可得到半径的长。故选B

2. (2024·温州期中)如果一个三角形的外心在三角形的外部,那么这个三角形一定是(C).
A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法确定

答案： 2.C

3. (2025·金华东阳期中)已知 M(1,2),N(3,-3),P(x,y)三点可以确定一个圆,则以下点 P 坐标不满足要求的是(C).
A.(3,5)
B.(-3,5)
C.(-1,7)
D.(1,-3)

答案： 3.C　[解析]设直线MN的表达式为y=kx+b。
∴{k + b = 2,3k + b = -3，解{k = -$\frac{5}{2}$,b = $\frac{9}{2}$}
∴y = -$\frac{5}{2}$x + $\frac{9}{2}$
当x = 3时，y = -3 ≠ 5；
当x = -3时，y = 12 ≠ 5；
当x = -1时，y = 7；
当x = 1时，y = 2 ≠ -3。
∴点(-1,7)在直线MN上，该三点不能构成圆。
故选C。
归纳总结　本题考查了确定圆的条件，关键是掌握不在同一条直线上的三个点确定一个圆。

4. (2025·北京 166 中期中)如图,在平面直角坐标系 xOy 中,若△ABC 的三个顶点都在格点上,则△ABC 的外心坐标为______.

答案：
4.(3,2)　[解析]如图所示，△ABC外接圆圆心的坐标为(3,2)。

5. 如图,在正方形网格中,每个小正方形的边长为 1,当三角形的三个顶点都在正方形网格线的交点上时,我们称三角形为格点三角形. 在图中标出△ABC 的外接圆的圆心 O 的位置.

答案：
5.如图，点O即为所求。

6. (2024·石家庄一模)如图,在平面直角坐标系中,点 A,B,C 的坐标分别为(1,4),(5,4),(1,-2),则△ABC 外接圆的圆心坐标是( ).

A.(2,3)
B.(3,2)
C.(1,3)
D.(3,1)

答案：
6.D　[解析]如图，根据外心的定义，则作弦AB，AC的垂直平分线，交点O₁即为圆心，且坐标是(3,1)。故选D。

7. 实验班原创 如图,点 O 是△ABC 的外心,连结 OA,OB,若∠OBA= 25°,则∠AOB 的度数为______.

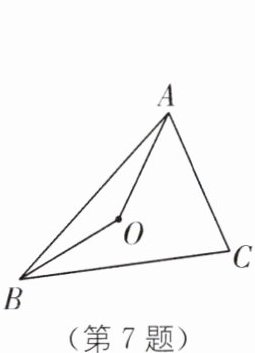
130°

答案： 7.130°　[解析]
∵点O是△ABC的外心，
∴OA = OB，
∴△AOB是等腰三角形。
∵∠OBA = 25°，
∴∠AOB = 180° - 25°×2 = 130°。

8. (2025·黑龙江鸡西二中期末)如图所示,点 A,B,C 均在 6×6 的正方形网格格点上,过 A,B,C 三点的外接圆除经过 A,B,C 三点外还能经过的格点数为______.

答案：
8.5　[解析]如图，连结AB，BC，分别作AB，BC的垂直平分线，两直线的交点为O。

以O为圆心，OA为半径作圆，则⊙O即为过A，B，C三点的圆，由图可知，⊙O还经过点D，E，F，G，H这5个格点。

9. (2024·青海海东期末)如图,在△ABC 中,AB= AC,AD 是∠BAC 的平分线,EF 是 AC 的垂直平分线,交 AD 于点 O. 若 OA= 3,则△ABC 外接圆的面积为______.

答案：
9.9π　[解析]如图，连结OB，OC。

∵AB = AC，AD是∠BAC的平分线，
∴AD是边BC的垂直平分线，
∴OB = OC。
∵EF是AC的垂直平分线，
∴OA = OC，
∴OA = OB = OC，
∴△ABC外接圆的圆心是O，半径是OA。
又OA = 3，
∴△ABC外接圆的面积为π×3² = 9π。
思路引导　连结OB，OC，先证明OB = OC，再由EF是AC的垂直平分线，可得OA = OB = OC，从而推出△ABC外接圆的圆心是O，半径是OA，即可得到△ABC外接圆的面积。

10. (2025·温州鹿城区期中)在综合实践“研究轴对称图形”活动中,小明同学发现一个有趣的现象：过抛物线与坐标轴的三个交点的圆的圆心总落在抛物线的对称轴上. 小明想：如果知道抛物线的表达式,那就一定能求出过抛物线与坐标轴三个交点的圆的半径. 请计算,若已知抛物线$ y= x^2-2x-3,$设该抛物线与 x 轴相交于 A,B 两点,与 y 轴交于点 C,那么经过 A,B,C 三点的圆的半径长是______.

答案：
10.$\sqrt{5}$　[解析]在y = x² - 2x - 3中，令y = 0，则x² - 2x - 3 = 0，
解得x = 3或x = -1，
∴A(-1,0)，B(3,0)，
∴AB = 4。
令x = 0，则y = -3，
∴C(0,-3)，
∴OC = 3。
设经过A，B，C三点的圆的圆心为M，
如图，过点M作ME⊥AB于点E，MF⊥OC于点F。

∴BE = $\frac{1}{2}$AB = 2，OF = EM，FM = OE = 1。
设OF = EM = x，
∴CF = 3 - x。
∵CM = BM，
∴CF² + FM² = BE² + EM²，
∴(3 - x)² + 1² = 2² + x²，
∴x = 1，
∴EM = 1，
∴BM = $\sqrt{EM² + BE²}$ = $\sqrt{5}$，
∴经过A，B，C三点的圆的半径长是$\sqrt{5}$。