《2025年实验班提优训练九年级数学上册浙教版》

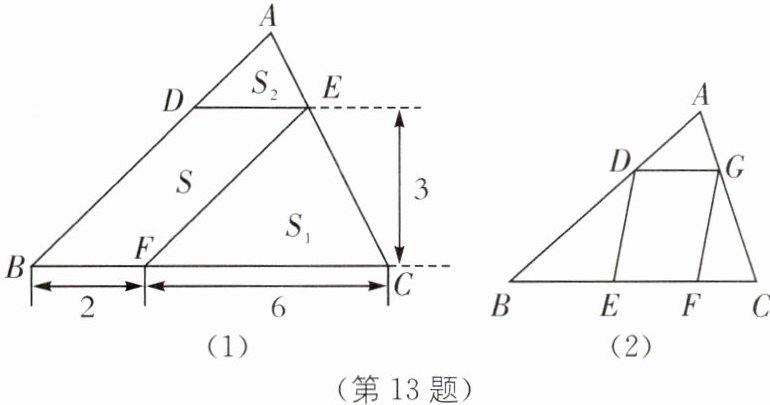
13. (1)如图(1),在△ABC 中,DE//BC 分别交 AB,AC 于 D,E 两点,过点 E 作 EF//AB 交 BC 于点 F. 请按图示数据填空:
四边形 DBFE 的面积 S= 6,
△EFC 的面积$S_1$= 9,
△ADE 的面积$S_2$= 1;
探究发现:
(2)在(1)中,若 BF= a,FC= b,DE 与 BC 间的距离为 h. 请证明:$S^2= 4S_1S_2$;
拓展迁移:
(3)如图(2),□DEFG 的四个顶点在△ABC 的三边上,若△ADG,△DBE,△GFC 的面积分别为 2,5,3,试利用(2)中的结论求△ABC 的面积.

（2）
∵$DE// BC$，$EF// AB$，
∴四边形DBFE为平行四边形，$\angle AED=\angle C$，$\angle A=\angle CEF$.
∴$\triangle ADE\backsim \triangle EFC$.
∴$\frac{S_{2}}{S_{1}}=(\frac{DE}{FC})^{2}=\frac{a^{2}}{b^{2}}$.
∵$S_{1}=\frac{1}{2}bh$，
∴$S_{2}=\frac{a^{2}}{b^{2}}\cdot S_{1}=\frac{a^{2}h}{2b}$.
∴$4S_{1}S_{2}=4×\frac{1}{2}bh\cdot\frac{a^{2}h}{2b}=(ah)^{2}$.又$S = ah$，
∴$S^{2}=4S_{1}S_{2}$.
（3）过点G作$GH// AB$交BC于点H，则四边形DBHG为平行四边形.
∴$\angle GHC=\angle B$，$BD = HG$，$DG = BH$.
∵四边形DEFG为平行四边形，
∴$DG = EF$.
∴$BH = EF$.
∴$BE = HF$.
∴$\triangle DBE\cong \triangle GHF$.
∴$\triangle GHC$的面积为$5 + 3=8$.由（2），得$□ DBHG$的面积为$\sqrt{4×2×8}=8$，
∴$\triangle ABC$的面积为$2 + 8 + 8=18$.

答案： （1）6 9 1
（2）
∵$DE// BC$，$EF// AB$，
∴四边形DBFE为平行四边形，$\angle AED=\angle C$，$\angle A=\angle CEF$.
∴$\triangle ADE\backsim \triangle EFC$.
∴$\frac{S_{2}}{S_{1}}=(\frac{DE}{FC})^{2}=\frac{a^{2}}{b^{2}}$.
∵$S_{1}=\frac{1}{2}bh$，
∴$S_{2}=\frac{a^{2}}{b^{2}}\cdot S_{1}=\frac{a^{2}h}{2b}$.
∴$4S_{1}S_{2}=4×\frac{1}{2}bh\cdot\frac{a^{2}h}{2b}=(ah)^{2}$.又$S = ah$，
∴$S^{2}=4S_{1}S_{2}$.
（3）过点G作$GH// AB$交BC于点H，则四边形DBHG为平行四边形.
∴$\angle GHC=\angle B$，$BD = HG$，$DG = BH$.
∵四边形DEFG为平行四边形，
∴$DG = EF$.
∴$BH = EF$.
∴$BE = HF$.
∴$\triangle DBE\cong \triangle GHF$.
∴$\triangle GHC$的面积为$5 + 3=8$.由（2），得$□ DBHG$的面积为$\sqrt{4×2×8}=8$，
∴$\triangle ABC$的面积为$2 + 8 + 8=18$.

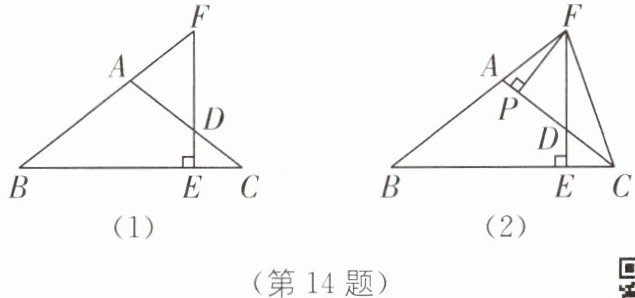
14. (2024·赤峰中考)数学课上,老师给出以下条件,请同学们经过小组讨论,提出探究问题. 如图(1),在△ABC 中,AB= AC,点 D 是 AC 上的一个动点,过点 D 作 DE⊥BC 于点 E,延长 ED 交 BA 的延长线于点 F.
请你解决下面各组提出的问题:
(1)求证:AD= AF.
(2)某小组探究发现,当$\frac{AD}{DC}= \frac{1}{3}$时,$\frac{DF}{DE}= \frac{2}{3}$;当$\frac{AD}{DC}= \frac{4}{5}$时,$\frac{DF}{DE}= \frac{8}{5}$,请你继续探究:
①当$\frac{AD}{DC}= \frac{7}{6}$时,$\frac{DF}{DE}= $______;
②当$\frac{AD}{DC}= \frac{m}{n}$时,$\frac{DF}{DE}= $______.(用含 m,n 的式子表示)
(3)[拓展应用]在图(1)中,过点 F 作 FP⊥AC,垂足为 P,连结 CF,得到图(2),当点 D 运动到使∠ACF= ∠ACB 时,若$\frac{AD}{DC}= \frac{m}{n}$,求$\frac{AP}{AD}$的值(用含 m,n 的式子表示).

答案：
（1）
∵$AB = AC$，
∴$\angle B=\angle C$.
∵$DE\perp BC$，
∴$\angle BED=\angle CED = 90^{\circ}$，
∴$\angle B+\angle F=\angle C+\angle EDC = 90^{\circ}$，
∴$\angle F=\angle EDC$.
∵$\angle ADF=\angle EDC$，
∴$\angle F=\angle ADF$，
∴$AD = AF$.
（2）①$\frac{7}{3}$ [解析]如图（1），过点A作$AG// CE$，则$AG\perp DF$，

∴$\triangle AGD\backsim \triangle CED$，
∴$\frac{GD}{DE}=\frac{AD}{DC}=\frac{7}{6}$.
∵$AF = AD$，
∴$GF = GD$，
∴$\frac{DF}{DE}=2\cdot\frac{GD}{DE}=\frac{7}{3}$.
②$\frac{2m}{n}$ [解析]由①可得$\frac{DF}{DE}=2\cdot\frac{GD}{DE}=\frac{2m}{n}$.
（3）设$\angle ABC=\angle ACB=\angle ACF=\alpha$，在$\mathrm{Rt}\triangle FAP$和$\mathrm{Rt}\triangle FCE$中，$\angle FAP=\angle FCE = 2\alpha$.又$\angle FPA=\angle FEC$，
∴$\triangle FPA\backsim \triangle FEC$.
∴$\frac{AP}{CE}=\frac{AF}{CF}$.
∴$\frac{AP}{AF}=\frac{CE}{CF}$.
∵$AD = AF$，

∴$\frac{AP}{AD}=\frac{CE}{CF}$.如图（2），过点F作$FM// BC$交CA的延长线于点M，
∵$\angle ACB=\angle ACF=\angle M$，
∴$CF = MF$，同理$AM = AF = AD$，
∴$\frac{CE}{CF}=\frac{CE}{MF}=\frac{CD}{MD}=\frac{CD}{2AD}=\frac{n}{2m}$.
∴$\frac{AP}{AD}=\frac{n}{2m}$.