《2025年实验班提优训练九年级数学上册浙教版》

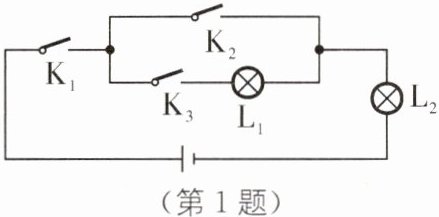
1.(2024·乌鲁木齐一模)物理某一实验的电路图如图所示,其中$K_1,K_2,K_3$为电路开关$,L_1,L_2$为能正常发光的灯泡.任意闭合开关$K_1,K_2,K_3$中的两个,那么能让两盏灯泡同时发光的概率为( ).


A.$\frac{1}{3}$
B.$\frac{2}{3}$
C.$\frac{1}{2}$
D.$\frac{1}{4}$

答案：
A [解析]画树状图如图.
　　　　　　
共有6种等可能的结果，能让两盏灯泡同时发光的有2种情况，
∴能让两盏灯泡同时发光的概率为$ P=\frac{2}{6}=\frac{1}{3} $.
故选A.

2. 某水果超市为了吸引顾客来店购物,设立了一个如图所示的可以自由转动的转盘,开展有奖购物活动,顾客购买商品满200元就能获得一次转动转盘的机会,当转盘停止时,指针落在“一袋苹果”的区域就可以获得一袋苹果;指针落在“一袋橘子”的区域就可以获得一袋橘子.若转动转盘2000次,指针落在“一袋橘子”区域的次数有600次,则某位顾客转动转盘一次,获得一袋橘子的概率大约是(A).

A.0.3
B.0.7
C.0.4
D.0.2

答案： A [解析]用频率估计概率，转动转盘2000次，指针落在“一袋橘子”区域的次数有600次，频率为$ 600÷2000 = 0.3 $，因此估计概率为0.3，即转动转盘一次，获得一袋橘子的概率大约为0.3.故选A.

3.(2025·四川成都四十九中期中)从3,0,-1,-2,-3这五个数中,随机抽取一个数作为m的值,则使函数$y= (5-m^{2})x$的图象经过第一、三象限,且使关于x的方程$(m+1)x^{2}+mx+1= 0$有实数根的概率是$\frac{2}{5}$.

答案： $ \frac{2}{5} $ [解析]
∵所得函数的图象经过第一、三象限，
∴$ 5 - m^{2} ＞ 0 $，
∴$ m^{2} ＜ 5 $，
∴3，0， - 1， - 2， - 3中，3和 - 3均不符合题意，
将$ m = 0 $代入$ (m + 1)x^{2} + mx + 1 = 0 $中，得$ x^{2} + 1 = 0 $，$ \Delta = - 4 ＜ 0 $，无实数根；
将$ m = - 1 $代入$ (m + 1)x^{2} + mx + 1 = 0 $中，得$ - x + 1 = 0 $，$ x = 1 $，有实数根；
将$ m = - 2 $代入$ (m + 1)x^{2} + mx + 1 = 0 $中，得$ x^{2} + 2x - 1 = 0 $，$ \Delta = 4 + 4 = 8 ＞ 0 $，有实数根.
故方程有实数根的概率是$ \frac{2}{5} $.

4. 第31届世界大学生夏季运动会将在四川成都举行.小杰和哥哥都很想去观看羽毛球比赛,爸爸只买到了一张门票,最后商定通过转盘游戏决定谁去观看比赛.游戏规则是:转动如图所示的转盘,转盘停止后,若转盘指针指向红色,小杰去;若转盘指针指向蓝色或黄色,哥哥去(若指针恰好指向白色或指向分割线,则重新转动).求小杰去观看羽毛球比赛的概率.

答案： 由题意，知转盘中每一个扇形面积相同，共有9份，其中红色占4份，白色占1份，蓝色和黄色共占4份，再结合若指针恰好指向白色或指向分割线，则重新转动，
∴$ P $(小杰去观看羽毛球比赛)$ =\frac{4}{9 - 1}=\frac{1}{2} $.

5. 有七张正面分别标有数字-3,-2,-1,0,1,2,3的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程$x^{2}-2(a-1)x+a(a-3)= 0$有两个不相等的实数根,且以x为自变量的二次函数$y= x^{2}-(a^{2}+1)x-a+2$的图象不经过点(1,0)的概率是(B).
A.$\frac{2}{7}$
B.$\frac{3}{7}$
C.$\frac{4}{7}$
D.$\frac{6}{7}$

答案： B [解析]$ \Delta = [-2(a - 1)]^{2} - 4a(a - 3) = 4a + 4 ＞ 0 $，解得$ a ＞ - 1 $，
∴使关于x的一元二次方程$ x^{2} - 2(a - 1)x + a(a - 3) = 0 $有两个不相等的实数根的数有0，1，2，3.
当二次函数$ y = x^{2} - (a^{2} + 1)x - a + 2 $的图象经过点(1，0)时，$ 1 - (a^{2} + 1) - a + 2 = 0 $，
解得$ a_{1} = - 2 $，$ a_{2} = 1 $.
∴使关于x的一元二次方程$ x^{2} - 2(a - 1)x + a(a - 3) = 0 $有两个不相等的实数根，且以x为自变量的二次函数$ y = x^{2} - (a^{2} + 1)x - a + 2 $的图象不经过点(1，0)的数字为0，2，3，
∴所述事件的概率为$ \frac{3}{7} $.故选B.

6. 中考新考法 新定义问题 (2024·阜阳一模)我们把十位上的数字比个位、百位上的数字都要大的三位数叫做“凸数”,如:571就是一个“凸数”.若十位上的数字为4,则从2,3,5,6中任取两个不同的数,能与4组成“凸数”的概率为(A).
A.$\frac{1}{6}$
B.$\frac{3}{5}$
C.$\frac{1}{2}$
D.$\frac{1}{3}$

答案： A [解析]列表如下:
　　　　　　2　　　　3　　　　5　　　　6
　　　　2　　　　　(2,3)　　(2,5)　　(2,6)
　　　　3(3,2)　　　　　　(3,5)　　(3,6)
　　　　5(5,2)　　(5,3)　　　　　　(5,6)
　　　　6(6,2)　　(6,3)　　(6,5)
共有12种等可能的结果，其中能与4组成“凸数”的结果为(2,3)，(3,2)，共2种，
∴能与4组成“凸数”的概率为$ \frac{2}{12}=\frac{1}{6} $.故选A.