《2025年实验班提优训练九年级数学上册浙教版》

1.(2024·河北模拟)已知二次函数$y= (x-h)^{2}+1$($h$为常数)在自变量$x的值满足1\leqslant x\leqslant 3$的情况下,与其对应的函数值$y$的最小值为5,则$h$的值为(B).
A.1或-5
B.-1或5
C.1或-3
D.1或3

答案： B [解析]
∵当x=h时,y取最小值为1,
∴h的值不可能在1到3之间.
当h＜1≤x≤3时，
当x=1时,y取得最小值5,
∴(1 - h)²+1=5，
解得h = - 1或h = 3(不合题意,舍去);
当1≤x≤3＜h时，
当x=3时,y取得最小值5,
∴(3 - h)²+1=5，
解得h = 5或h = 1(不合题意,舍去).故选B

变式1.1 (2024·贵港港南区四模)已知二次函数$y= mx^{2}-2mx+2(m≠0)在-2\leqslant x＜2$时有最小值-2,则$m$等于(B).
A.-4或$-\frac{1}{2}$
B.4或$-\frac{1}{2}$
C.-4或$\frac{1}{2}$
D.4或$\frac{1}{2}$

答案： B [解析]
∵二次函数y = mx² - 2mx + 2 = m(x - 1)² - m + 2,
∴对称轴为直线x = 1.
①若m＞0,则抛物线开口向上，
当x = 1时,有最小值y = - m + 2 = - 2,解得m = 4;
②若m＜0,则抛物线开口向下,
∵对称轴为直线x = 1,在 - 2≤x≤2时有最小值 - 2,
∴x = - 2时,有最小值y = 9m - m + 2 = - 2,
解得m = -$\frac{1}{2}$.故选B

变式1.2 (2025·辽宁大连西岗区期中)已知二次函数$y= -x^{2}+2mx-m^{2}+3在m-1\leqslant x\leqslant m+2$的范围内有最小值,则这个最小值是-1.

答案： - 1 [解析]二次函数y = - x²+2mx - m²+3的对称轴是直线x = m.
∵a = - 1＜0,
∴抛物线开口向下.
∵二次函数在m - 1≤x≤m + 2的范围内有最小值，
∴x = m + 2时,y取值最小,最小值为 - (m + 2)²+2m·(m + 2) - m²+3 = - m² - 4m - 4+2m²+4m - m²+3 = - 1.

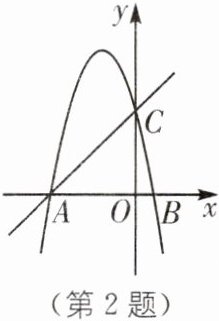
2.(2025·广东惠州惠城区惠港中学月考改编)如图,在平面直角坐标系中,抛物线$y= -x^{2}-4x+c与x轴交于点A,B$(点$A在点B$左侧),与$y轴交于点C$,且点$A的坐标为(-5,0)$.
(1)求点$C$的坐标；
(2)若点$P$是第二象限内抛物线上一动点,求点$P到直线AC$距离的最大值.

答案：
(1)把点A的坐标( - 5,0)代入y = - x² - 4x + c，
得 - 25+20 + c = 0,解得c = 5,
∴点C的坐标为(0,5).
(2)由
(1)知,抛物线的表达式为y = - x² - 4x + 5，
令y = - x² - 4x + 5 = 0,解得x = 1或 - 5,
∴点B的坐标为(1,0).
如图,过点P作PE⊥AC于点E,过点P作PF⊥x轴交AC于点H.
∵A( - 5,0),C(0,5),
∴OA = OC,
∴△AOC是等腰直角三角形，
∴∠CAO = 45°.
∵PF⊥x轴,
∴∠AHF = 45° = ∠PHE,
∴△PHE是等腰直角三角形，
∴PE = HE,
∴在Rt△PHE中,由勾股定理得PH² = PE²+HE² = 2PE²,
∴PE = $\frac{PH}{\sqrt{2}}$,
∴当PH最大时,PE最大.
设直线AC表达式为y = kx + 5，
将A( - 5,0)代入,得0 = - 5k + 5,解得k = 1，
∴直线AC的表达式为y = x + 5.
设P(m, - m² - 4m + 5)( - 5＜m＜0),则H(m,m + 5),
∴PH = ( - m² - 4m + 5) - (m + 5)= - (m + $\frac{5}{2}$)²+$\frac{25}{4}$.
∵a = - 1＜0,
∴当m = - $\frac{5}{2}$时,PH的最大值为$\frac{25}{4}$，
∴PE = $\frac{25}{4\sqrt{2}}$ = $\frac{25\sqrt{2}}{8}$，
∴此时PE的最大值为$\frac{25\sqrt{2}}{8}$,点P到直线AC的距离值最大，即点P到直线AC距离的最大值为$\frac{25\sqrt{2}}{8}$.