《2025年实验班提优训练九年级数学上册浙教版》

19. (1)如图(1)所示,$△ABC$是正三角形,E,D 分别是 CB 和 AC 延长线上的点,且$BE= CD$,连结 DB 并延长,交 AE 于点 F,求$∠AFB$的度数;
(2)若将(1)中正三角形 ABC 改成正n边形 ABCM…N,如图(2)所示,其他条件均不变,用含字母 n 的代数式表示$∠AFB$的度数,并说明理由.
]

答案：
(1)在$△ABC$中，$∠ABC = ∠ACB = 60^{\circ },AB = BC,$
∴$∠ABE = ∠BCD.$
在$△ABE$和$△BCD$中，
$\begin{cases}BE = CD\\∠ABE = ∠BCD\\AB = BC\end{cases}$
∴$△ABE\cong △BCD,$
∴$∠E = ∠D.$
∵$∠EBF = ∠CBD,$
∴$∠AFB = ∠E + ∠EBF = ∠D + ∠CBD = ∠ACB = 60^{\circ }.$
(2)$∠AFB = ∠MCB=\frac {(n - 2)×180^{\circ }}{n}$.理由如下:
在正n边形ABCM…N中，
$∠ABC = ∠MCB=\frac {(n - 2)×180^{\circ }}{n},AB = BC,$
∴$∠ABE = ∠BCD.$
在$△ABE$和$△BCD$中，
$\begin{cases}BE = CD\\∠ABE = ∠BCD\\AB = BC\end{cases}$
∴$△ABE\cong △BCD,$
∴$∠E = ∠D.$
∵$∠EBF = ∠CBD,$
∴$∠AFB = ∠E + ∠EBF = ∠D + ∠CBD = ∠MCB=\frac {(n - 2)×180^{\circ }}{n}.$

20. 转化思想 中考新考法 类比猜想 如图(1)(2)(3),点 E,D 分别是正三角形 ABC,正方形 ABCM,正五边形 ABCMN 中以点 C 为顶点的相邻两边上的点,且$BE= CD$,DB 交 AE 于点 P.
(1)求图(1)中$∠APD$的度数;
(2)图(2)中,$∠APD$的度数为$90^{\circ }$,图(3)中,$∠APD$的度数为$108^{\circ }$;
(3)根据前面的探索,你能否将本题推广到一般的正n边形情况？若能,写出推广的问题和结论;若不能,请说明理由.
]


(1)∵$△ABC$是等边三角形，
∴$AB = BC,∠ABE = ∠BCD = 60^{\circ }.$
∵$BE = CD,$
∴$△ABE\cong △BCD.$
∴$∠BAE = ∠CBD.$
∴$∠APD = ∠ABP + ∠BAE = ∠ABP + ∠CBD = ∠ABE = 60^{\circ }.$
(3)能.点E，D分别是正n边形中以点C为顶点的相邻两边上的点，且$BE = CD$，BD与AE交于点P，则$∠APD$的度数为$\frac {(n - 2)\cdot {180}^{\circ }}{n}.$

答案：
(1)
∵$△ABC$是等边三角形，
∴$AB = BC,∠ABE = ∠BCD = 60^{\circ }.$
∵$BE = CD,$
∴$△ABE\cong △BCD.$
∴$∠BAE = ∠CBD.$
∴$∠APD = ∠ABP + ∠BAE = ∠ABP + ∠CBD = ∠ABE = 60^{\circ }.$
(2)$90^{\circ }$，$108^{\circ }$
(3)能.点E，D分别是正n边形中以点C为顶点的相邻两边上的点，且$BE = CD$，BD与AE交于点P，则$∠APD$的度数为$\frac {(n - 2)\cdot {180}^{\circ }}{n}.$

21.(2024·青岛中考)为筹备运动会,小松制作了如图所示的宣传牌,在正五边形 ABCDE 和正方形 CDFG 中,CF,DG 的延长线分别交 AE,AB 于点 M,N,则$∠FME$的度数是(B).

A.$90^{\circ }$
B.$99^{\circ }$
C.$108^{\circ }$
D.$135^{\circ }$
]

答案： B　[解析]
∵五边形ABCDE是正五边形，
∴$∠CDE = ∠E=\frac {(5 - 2)×180^{\circ }}{5}=108^{\circ }.$
∵四边形CDFG为正方形，
∴$∠CDF = 90^{\circ },∠CFD = 45^{\circ },$
∴$∠FDE = 108^{\circ }-90^{\circ }=18^{\circ },∠DFM = 180^{\circ }-45^{\circ }=135^{\circ },$
∴$∠FME = 360^{\circ }-18^{\circ }-135^{\circ }-108^{\circ }=99^{\circ }.$
故选B.

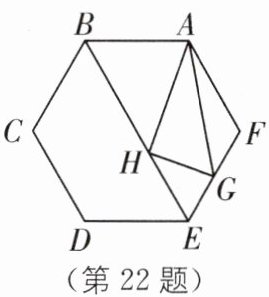
22.(2024·绵阳中考)如图,在边长为 2 的正六边形 ABCDEF 中,连结 BE,点 H 在 BE 上运动,点 G 为 EF 的中点,当$△AGH$的周长最小时,$AH+GH= ( ).$

A.$2\sqrt {3}$
B.$\sqrt {13}$
C.12
D.13

答案：
B　[解析]如图，
要使$△AGH$的周长最小，即$AH + HG$最小，
　　　　　　　　　　　　　　　　
利用正六边形的性质可得点G关于BE的对称点为点$G'$，连结$AG'$交BE于点$H'$，连结$AE,H'G,$
那么有$H'G = H'G',AH' + GH' = AH' + H'G'$最小.
当$△AGH$周长最小时，点$A,H',G'$共线，此时$AH' + GH' = AG'.$
∵$∠F = 120^{\circ },AF = EF = 2,$
∴$AE = 2\sqrt {3}.$
∵$∠AEG' = 90^{\circ },EG'=\frac {1}{2}DE = 1,$
∴$AG'=\sqrt {1^{2}+(2\sqrt {3})^{2}}=\sqrt {13}.$
故当$△AGH$的周长最小时，$AH + GH=\sqrt {13}.$
故选B.