第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
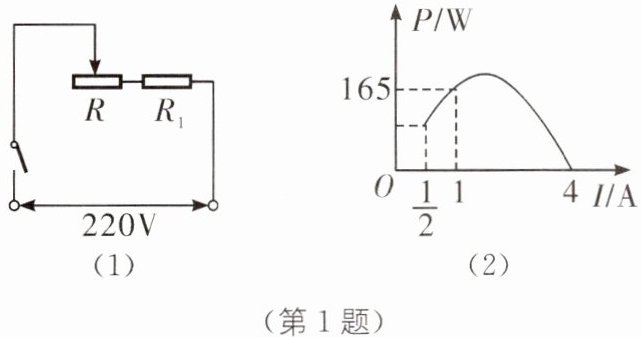
1. (2024·西安模拟)某物理兴趣小组对一款饮水机的工作电路展开研究,如图(1),将变阻器 R 的滑片从一端滑到另一端,绘制出变阻器 R 消耗的电功率 P 随电流 I 变化的关系图象,如图(2)所示,且该图象是经过原点的一条抛物线的一部分,则变阻器 R 消耗的电功率 P 最大为(
A.160 W
B.180 W
C.200 W
D.220 W
D
).
A.160 W
B.180 W
C.200 W
D.220 W
答案:
D [解析] 由图象是经过原点的一条抛物线的一部分,设抛物线表达式为 $ P=aI^{2}+bI $,把(1,165),(4,0)代入,得$ \begin{cases} a+b=165, \\ 16a+4b=0, \end{cases} $解得$ \begin{cases} a=-55, \\ b=220. \end{cases} $
∴抛物线表达式为 $ P=-55I^{2}+220I=-55(I-2)^{2}+220 $.
∵-55<0,
∴当$ I=2 $时,P取最大值220,
∴变阻器R消耗的电功率P最大为220 W.故选D.
∴抛物线表达式为 $ P=-55I^{2}+220I=-55(I-2)^{2}+220 $.
∵-55<0,
∴当$ I=2 $时,P取最大值220,
∴变阻器R消耗的电功率P最大为220 W.故选D.
2. (2024·嘉兴期末)某车的刹车距离 y(m)与开始刹车时的速度 x(m/s)满足二次函数 $ y= 0.04x^{2} $(x>0),若该车某次的刹车距离为 9 m,则开始刹车时的速度为
15
m/s.
答案:
15 [解析] 当刹车距离为9m时,即可得$ y=9 $.将$ y=9 $代入$ y=0.04x^{2} $,得$ 9=0.04x^{2} $,解得$ x_{1}=15,x_{2}=-15 $(舍去),故开始刹车时的速度为15 m/s.
易错警示 二次函数转化为二次方程时,需要注意未知数的取值范围.
易错警示 二次函数转化为二次方程时,需要注意未知数的取值范围.
3. 跨学科 小球运动 根据物理学规律,如果不考虑空气阻力,以 40 m/s 的速度将小球沿与地面成 30°角的方向击出,小球的飞行高度 h(单位:m)与飞行时间 t(单位:s)之间的函数关系是:$ h= -5t^{2}+20t $,则小球运动中的最大高度是
20
m.
答案:
20 [解析]$ h=-5t^{2}+20t=-5(t-2)^{2}+20 $.
∵-5<0,
∴当$ t=2 $时,h有最大值,最大值为20.
归纳总结 求最值的方法可用配方法或公式法.一般地,当$ a>0 $(或$ a<0 $)时,抛物线$ y=ax^{2}+bx+c(a≠0) $的顶点是最低(高)点,也就是说,当$ x=-\frac{b}{2a} $时,二次函数$ y=ax^{2}+bx+c(a≠0) $有最小(大)值$ \frac{4ac-b^{2}}{4a} $.
∵-5<0,
∴当$ t=2 $时,h有最大值,最大值为20.
归纳总结 求最值的方法可用配方法或公式法.一般地,当$ a>0 $(或$ a<0 $)时,抛物线$ y=ax^{2}+bx+c(a≠0) $的顶点是最低(高)点,也就是说,当$ x=-\frac{b}{2a} $时,二次函数$ y=ax^{2}+bx+c(a≠0) $有最小(大)值$ \frac{4ac-b^{2}}{4a} $.
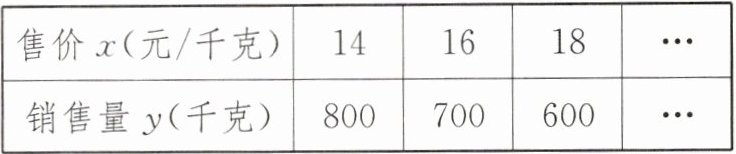
4. 新情境 销售有机大米 金秋十月,某农业合作社有机水稻再获丰收,加工成有机大米后通过实体和电商两种渠道进行销售.该有机大米成本为每千克 14 元,销售价格不低于成本,且不超过 25 元/千克,根据各销售渠道的反馈,发现该有机大米一天的销售量 y(千克)是该天的售价 x(元/千克)的一次函数,部分情况如下表:
|售价 x(元/千克)|14|16|18|…|
|销售量 y(千克)|800|700|600|…|
(1)求一天的销售量 y(千克)与售价 x(元/千克)之间的函数表达式并写出 x 的取值范围.
(2)若某天销售这种大米获利 2400 元,那么这天该大米的售价为多少?
(3)该有机大米售价定为多少时,当天获利 w 最大?最大利润为多少?
|售价 x(元/千克)|14|16|18|…|
|销售量 y(千克)|800|700|600|…|

(1)求一天的销售量 y(千克)与售价 x(元/千克)之间的函数表达式并写出 x 的取值范围.
(2)若某天销售这种大米获利 2400 元,那么这天该大米的售价为多少?
(3)该有机大米售价定为多少时,当天获利 w 最大?最大利润为多少?
答案:
(1)设一天的销售量y(千克)与该天的售价x(元/千克)之间的函数表达式为$ y=kx+b $,将(14,800),(16,700)代入,得$ \begin{cases} 14k+b=800, \\ 16k+b=700, \end{cases} $解得$ \begin{cases} k=-50, \\ b=1500. \end{cases} $故一天的销售量y(千克)与该天的售价x(元/千克)之间的函数表达式为$ y=-50x+1500(14≤x≤25) $.
(2)由题意,得$ (-50x+1500)(x-14)=2400 $,解得$ x=26 $或$ x=18 $.
∵14≤x≤25,
∴$ x=18 $.故这天该大米的售价为18元/千克.
(3)设销售利润为w元.由题意,得$ w=y(x-14)=(-50x+1500)(x-14)=-50x^{2}+2200x-21000=-50(x-22)^{2}+3200 $.
∵-50<0,14≤x≤25,
∴$ x=22 $时,w取得最大值,最大值为3200.故该有机大米售价定为22元/千克时,当天获利最大,最大利润为3200元.
(1)设一天的销售量y(千克)与该天的售价x(元/千克)之间的函数表达式为$ y=kx+b $,将(14,800),(16,700)代入,得$ \begin{cases} 14k+b=800, \\ 16k+b=700, \end{cases} $解得$ \begin{cases} k=-50, \\ b=1500. \end{cases} $故一天的销售量y(千克)与该天的售价x(元/千克)之间的函数表达式为$ y=-50x+1500(14≤x≤25) $.
(2)由题意,得$ (-50x+1500)(x-14)=2400 $,解得$ x=26 $或$ x=18 $.
∵14≤x≤25,
∴$ x=18 $.故这天该大米的售价为18元/千克.
(3)设销售利润为w元.由题意,得$ w=y(x-14)=(-50x+1500)(x-14)=-50x^{2}+2200x-21000=-50(x-22)^{2}+3200 $.
∵-50<0,14≤x≤25,
∴$ x=22 $时,w取得最大值,最大值为3200.故该有机大米售价定为22元/千克时,当天获利最大,最大利润为3200元.
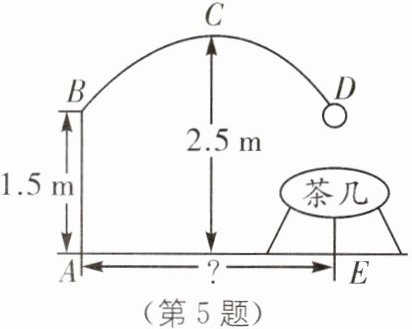
5. (2024·吉林长春外国语学校月考)如图是一款抛物线型落地灯筒示意图,防滑螺母 C 为抛物线支架的最高点,灯罩 D 距离地面 2.25 米,最高点 C 距灯柱 AB 的水平距离为 1.5 米,灯柱 AB 为 1.5 米,若茶几摆放在灯罩的正下方,则茶几到灯柱的距离 AE 为( ).
A.2.25 米
B.0.75 米
C.1.6 米
D.2.5 米

A.2.25 米
B.0.75 米
C.1.6 米
D.2.5 米
答案:
A [解析] 如图所示,以AE所在直线为x轴,AB所在直线为y轴建立平面直角坐标系. 根据题意,知抛物线的顶点C的坐标为(1.5,2.5).设抛物线的表达式为$ y=a(x-1.5)^{2}+2.5 $,将B(0,1.5)代入,得$ 2.25a+2.5=1.5 $,解得$ a=-\frac{4}{9} $,
根据题意,知抛物线的顶点C的坐标为(1.5,2.5).设抛物线的表达式为$ y=a(x-1.5)^{2}+2.5 $,将B(0,1.5)代入,得$ 2.25a+2.5=1.5 $,解得$ a=-\frac{4}{9} $,
∴抛物线的表达式为$ y=-\frac{4}{9}(x-\frac{3}{2})^{2}+\frac{5}{2} $.当$ y=2.25 $时,$ -\frac{4}{9}(x-\frac{3}{2})^{2}+\frac{5}{2}=\frac{9}{4} $,解得$ x=0.75 $(舍去)或$ x=2.25 $.所以茶几到灯柱的距离AE为2.25米.故选A.
方法诠释 将二次函数的实际应用转化为二次函数图象,运用待定系数法求函数表达式与点的坐标是解题关键.
A [解析] 如图所示,以AE所在直线为x轴,AB所在直线为y轴建立平面直角坐标系.
 根据题意,知抛物线的顶点C的坐标为(1.5,2.5).设抛物线的表达式为$ y=a(x-1.5)^{2}+2.5 $,将B(0,1.5)代入,得$ 2.25a+2.5=1.5 $,解得$ a=-\frac{4}{9} $,
根据题意,知抛物线的顶点C的坐标为(1.5,2.5).设抛物线的表达式为$ y=a(x-1.5)^{2}+2.5 $,将B(0,1.5)代入,得$ 2.25a+2.5=1.5 $,解得$ a=-\frac{4}{9} $,∴抛物线的表达式为$ y=-\frac{4}{9}(x-\frac{3}{2})^{2}+\frac{5}{2} $.当$ y=2.25 $时,$ -\frac{4}{9}(x-\frac{3}{2})^{2}+\frac{5}{2}=\frac{9}{4} $,解得$ x=0.75 $(舍去)或$ x=2.25 $.所以茶几到灯柱的距离AE为2.25米.故选A.
方法诠释 将二次函数的实际应用转化为二次函数图象,运用待定系数法求函数表达式与点的坐标是解题关键.
查看更多完整答案,请扫码查看


