《2025年实验班提优训练九年级数学上册浙教版》

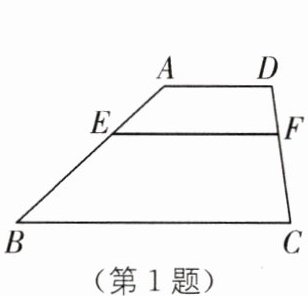
1. 教材 P126 作业题 T1·变式 (2024·哈尔滨中考)如图,在四边形 ABCD 中,AD//BC,点 E 在 AB 上,EF//AD 交 CD 于点 F,若 AE：BE= 1：2,DF= 3,则 FC 的长为(A).

A.6
B.3
C.5
D.9

答案： A　[解析]
∵在四边形ABCD中,AD//BC,EF//AD,
∴AD//EF//BC,
∴$\frac{AE}{EB}=\frac{DF}{FC}$,
　即$\frac{1}{2}=\frac{3}{FC}$,解得FC=6.故选A.

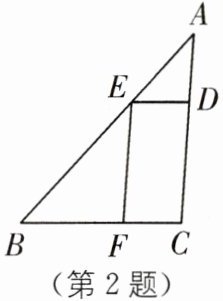
2. (2024·东营垦利区模拟)如图,在△ABC 中,DE//BC 分别交 AC,AB 于点 D,E,EF//AC 交 BC 于点 F,$\frac{AE}{BE}= \frac{2}{5}$,BF= 8,则 DE 的长为(A).

A.$\frac{16}{5}$
B.$\frac{16}{7}$
C.2
D.3

答案： A　[解析]
∵DE//BC,EF//AC,
∴四边形EFCD是平行四边形,
∴DE=CF,
　设DE=CF=x.
∵BF=8,
∴BC=BF+CF=8+x.
∵DE//BC,
∴$\frac{AE}{AB}=\frac{DE}{BC}$.
∵$\frac{AE}{BE}=\frac{2}{5}$,
∴$\frac{AE}{AB}=\frac{2}{7}$,
∴$\frac{DE}{BC}=\frac{2}{7}$,即$\frac{x}{8+x}=\frac{2}{7}$,
　解得$x=\frac{16}{5}$.经检验,$x=\frac{16}{5}$是该分式方程的解.故选A.

3. 教材 P125 例 1·拓展 (2025·台州期末)如图,直线 AD,BC 交于点 O,AB//EF//CD,若 AO= 2,OF= 1,FD= 2,则$\frac{AB}{CD}$的值为______.

$\frac{2}{3}$

答案： $\frac{2}{3}$　[解析]
∵OF=1,FD=2,
∴OD=OF+FD=1+2=3.
∵AB//EF//CD,
∴$\frac{AB}{CD}=\frac{OA}{OD}=\frac{2}{3}$.

4. (2025·湖南怀化期末)如图,已知 AB//CD//EF,那么下列结论正确的是(D).
A.$\frac{CD}{CB}= \frac{AD}{DF}$
B.$\frac{DF}{AD}= \frac{BC}{CE}$
C.$\frac{AD}{AF}= \frac{BE}{BC}$
D.$\frac{AD}{AF}= \frac{BC}{BE}$

答案： D

5. 如图,已知 AB//CD//EF,若$\frac{AC}{CE}= \frac{1}{2}$,则$\frac{DF}{BF}$的值为(C).

A.1
B.$\frac{1}{2}$
C.$\frac{2}{3}$
D.2

答案： C　[解析]
∵AB//CD//EF,$\frac{AC}{CE}=\frac{1}{2}$,
∴$\frac{AC}{CE}=\frac{BD}{DF}=\frac{1}{2}$,
∴$\frac{DF}{BF}=\frac{2}{3}$.故选C.
　知识拓展　三条平行线截两条直线，所得的对应线段成比例.

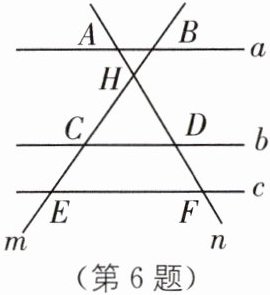
6. 数形结合思想 (2025·大连一模)如图,已知直线 a//b//c,分别交直线 m,n 于点 B,C,E,A,D,F,直线 m,n 相交于点 H,下列结论中错误的是( D ).

A.$\frac{BH}{HC}= \frac{AH}{HD}$
B.$\frac{AD}{DF}= \frac{BC}{CE}$
C.$\frac{AF}{DF}= \frac{BE}{CE}$
D.$\frac{HC}{HE}= \frac{HD}{DF}$

答案： D　[解析]已知直线a//b//c,分别交直线m,n于点B,C,E,A,D,F,
∴$\frac{BH}{HC}=\frac{AH}{HD}$,$\frac{AD}{DF}=\frac{BC}{CE}$,$\frac{AF}{DF}=\frac{BE}{CE}$,$\frac{HC}{HE}=\frac{HD}{HF}$,
∴选项A,B,C正确，不符合题意;D错误，符合题意;
　故选D.

7. 8字型 (宁波效实中学自主招生)如图,在△ABC 中,AD 是 BC 边上的高,K 为 AD 上一点,连结 BK 并延长交 AC 于点 E,连结 CK 并延长交 AB 于点 F. 求证：∠ADE= ∠ADF.
精题详解

答案：
如图，过点A作BC的平行线GH,分别交CF,DF，DE,BE的延长线于点G,M,N,H,
　　　　　　
∵GH//BC,
∴$\frac{AM}{BD}=\frac{AF}{FB}=\frac{AG}{BC}$,
∴$AM=\frac{BD\cdot AG}{BC}$.
　利用作平行线构造“8字型”得出等式
∵$\frac{AN}{CD}=\frac{AE}{EC}=\frac{AH}{BC}$,
∴$AN=\frac{CD\cdot AH}{BC}$,
∴$\frac{AM}{AN}=\frac{BD\cdot AG}{CD\cdot AH}$.
∵$\frac{AH}{BD}=\frac{KA}{KD}=\frac{AG}{CD}$,
∴BD·AG=CD·AH,
∴$\frac{AM}{AN}=1$,
∴AM=AN.
∵AD⊥BC,点M,N在直线GH上，
∴MN//BC,
∴AD⊥AM,
∴∠MAD=∠NAD=90°.
又AD=AD,
∴△ADM≌△ADN(SAS),
∴∠ADN=∠ADM,即∠ADE=∠ADF.