《2025年实验班提优训练九年级数学上册浙教版》

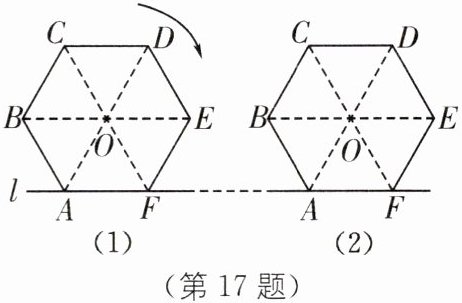
17. 如图,正六边形硬纸片$ ABCDEF $在桌面上由图(1)的起始位置沿直线$ l $不滑行地翻滚一周后到图(2)位置,若正六边形的边长为 2 cm,求正六边形的中心$ O $运动的路程.

答案： 根据题意，知每次滚动正六边形的中心就以正六边形的边长为半径旋转60°.
∵正六边形的边长为2cm,
∴中心O翻滚一次运动的路径长为$\frac{60\pi×2}{180}=\frac{2\pi}{3}$(cm).可知从题图
(1)运动到题图
(2)共重复进行了六次上述的滚动,
∴正六边形的中心O运动的路程为$6×\frac{2\pi}{3}=4\pi$(cm).

18. (2025·杭州拱墅区期末)如图,已知$ \odot O $的半径为 2,弦$ CD\perp 直径 AB $,垂足为$ E $,点$ F 在 \overset{\frown}{AC} $上(不与点$ A $,点$ C $重合),连结$ AF $,$ AC $,$ AD $,$ FC $.
(1)求证：$ AC= AD $.
(2)若$ \angle AFC= \frac{5}{3}\angle ACD $.
①求$ \angle ACD $的度数.
②当$ FC// AD $时,求$ \overset{\frown}{AF} $的长.

答案：

(1)
∵弦CD⊥直径AB,
∴$\overset{\frown}{AC}=\overset{\frown}{AD}$,
∴AC=AD.
(2)①
∵四边形AFCD内接于$\odot O$,
∴∠AFC+∠ADC=180°.
∵AC=AD,
∴∠ACD=∠ADC,
∵∠AFC=$\frac{5}{3}$∠ACD=$\frac{5}{3}$∠ADC,
∴∠ADC=67.5°,∠AFC=112.5°,
∴∠ACD=67.5°.②如图,连结OC,OD,
∵∠ADC=∠ACD=67.5°,
∴∠CAD=180°-2×67.5°=45°,
∴∠COD=90°.
∵FC//AD,
∴$\overset{\frown}{AF}=\overset{\frown}{CD}$.
∵$\overset{\frown}{CD}$的长为$\frac{90\pi×2}{180}=\pi$,
∴$\overset{\frown}{AF}$的长为π.

19. 如图,$ \triangle ABC $为等边三角形,边长为 1 cm. 将线段$ AC 绕点 A 顺时针旋转 120^{\circ} 至 AP_1 $,形成扇形$ D_1 $；将线段$ BP_1 绕点 B 顺时针旋转 120^{\circ} 至 BP_2 $,形成扇形$ D_2 $；将线段$ CP_2 绕点 C 顺时针旋转 120^{\circ} 至 CP_3 $,形成扇形$ D_3 $；将线段$ AP_3 绕点 A 顺时针旋转 120^{\circ} 至 AP_4 $,形成扇形$ D_4 $……设$ l_n 为扇形 D_n $的弧长($ n= 1,2,3,… $),回答下列问题：
(1)按要求填表：
| $ n $ | 1 | 2 | 3 | 4 |
| $ l_n $(cm) | $\frac{2}{3}\pi$ | $\frac{4}{3}\pi$ | 2π | $\frac{8}{3}\pi$ |

(2)按照上表所反映的规律,试估计$ n $至少为何值时,扇形$ D_n $的弧长能绕地球赤道一周？(设地球赤道半径为 6400 km)

n至少为1.92×10⁹.

答案：
(1)$\frac{2}{3}\pi$ $\frac{4}{3}\pi$ 2π $\frac{8}{3}\pi$
(2)n至少为1.92×10⁹.

20. 传统文化 轮动发石车 (2024·兰州中考)“轮动发石车”是我国古代的一种投石工具,在春秋战国时期被广泛应用,图(1)是陈列在展览馆的仿真模型. 图(2)是模型驱动部分的示意图,其中$ \odot M $,$ \odot N $的半径分别是 1 cm 和 10 cm,当$ \odot M $顺时针转动 3 周时,$ \odot N 上的点 P 随之旋转 n^{\circ} $,则$ n= $108.

答案： 108　[解析]
∵$\odot M$的周长为2πcm,
∴$\odot M$顺时针转动3周时，点P移动的弧长为6πcm,
∴$6\pi=\frac{n\pi×10}{180}$，解得n=108.