第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
7.(2025·杭州西湖区西溪中学期中)有一个圆形转盘,分黑色、白色两个区域.
(1)某人转动转盘,对指针域或白色区域进行了大量试验,得到数据如表:
|试验次数n(次)|10|100|2000|5000|10000|50000|100000|
|白色区域次数m(次)|3|34|680|1600|3405|16500|33000|
|落在白色区域频率$\frac{m}{n}$|0.3|0.34|0.34|0.32|0.34|0.33|0.33|
请你利用上述试验,估计转动该转盘指针落在白色区域的概率为______;
(2)若该圆形转盘白色扇形的圆心角为120°,黑色扇形的圆心角为240°,转动转盘两次,请用画树状图或列表的方法求指针一次落在白色区域,另一次落在黑色区域的概率.
(1)某人转动转盘,对指针域或白色区域进行了大量试验,得到数据如表:
|试验次数n(次)|10|100|2000|5000|10000|50000|100000|
|白色区域次数m(次)|3|34|680|1600|3405|16500|33000|
|落在白色区域频率$\frac{m}{n}$|0.3|0.34|0.34|0.32|0.34|0.33|0.33|
请你利用上述试验,估计转动该转盘指针落在白色区域的概率为______;
(2)若该圆形转盘白色扇形的圆心角为120°,黑色扇形的圆心角为240°,转动转盘两次,请用画树状图或列表的方法求指针一次落在白色区域,另一次落在黑色区域的概率.
答案:
(1)0.33 [解析]根据表格数据,知估计转动该转盘指针落在白色区域的概率为0.33;
(2)
∵白色扇形的圆心角为120°,黑色扇形的圆心角为240°,设白色扇形区域为白,黑色扇形区域为黑1,黑2,画树状图如图. 共有9种等可能的结果,其中指针一次落在白色区域,另一次落在黑色区域的结果有4种.$P(\text{一白一黑})=\frac{4}{9}$.故指针一次落在白色区域,另一次落在黑色区域的概率为$\frac{4}{9}$.
共有9种等可能的结果,其中指针一次落在白色区域,另一次落在黑色区域的结果有4种.$P(\text{一白一黑})=\frac{4}{9}$.故指针一次落在白色区域,另一次落在黑色区域的概率为$\frac{4}{9}$.
(1)0.33 [解析]根据表格数据,知估计转动该转盘指针落在白色区域的概率为0.33;
(2)
∵白色扇形的圆心角为120°,黑色扇形的圆心角为240°,设白色扇形区域为白,黑色扇形区域为黑1,黑2,画树状图如图.
 共有9种等可能的结果,其中指针一次落在白色区域,另一次落在黑色区域的结果有4种.$P(\text{一白一黑})=\frac{4}{9}$.故指针一次落在白色区域,另一次落在黑色区域的概率为$\frac{4}{9}$.
共有9种等可能的结果,其中指针一次落在白色区域,另一次落在黑色区域的结果有4种.$P(\text{一白一黑})=\frac{4}{9}$.故指针一次落在白色区域,另一次落在黑色区域的概率为$\frac{4}{9}$. 8."垃圾分类工作就是新时尚",为了改善生态环境,有效利用垃圾剩余价值,2020年起,衡阳市将生活垃圾分为四类:厨余垃圾、有害垃圾、可回收物、其他垃圾.某学习研究小组在对该市垃圾分类实施情况的调查中,绘制了生活垃圾分类扇形统计图,如图所示.
(1)图中其他垃圾所在的扇形的圆心角度数是______度;
(2)据统计,生活垃圾中可回收物每吨可创造经济总价值约为0.2万元.若衡阳市某天生活垃圾清运总量为500吨,请估计该天可回收物所创造的经济总价值是多少万元;
(3)为了调查学生对垃圾分类知识的了解情况,某校开展了相关知识竞赛,要求每班派2名学生参赛.甲班经选拔后,决定从2名男生和2名女生中随机抽取2名学生参加比赛,求所抽取的学生中恰好是一男一女的概率.
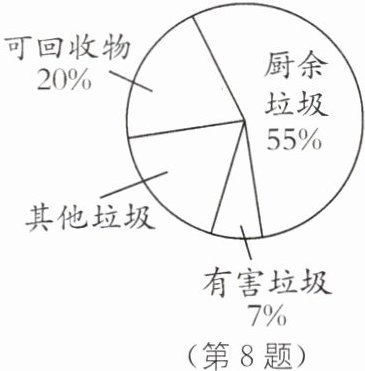
(1)图中其他垃圾所在的扇形的圆心角度数是______度;
(2)据统计,生活垃圾中可回收物每吨可创造经济总价值约为0.2万元.若衡阳市某天生活垃圾清运总量为500吨,请估计该天可回收物所创造的经济总价值是多少万元;
(3)为了调查学生对垃圾分类知识的了解情况,某校开展了相关知识竞赛,要求每班派2名学生参赛.甲班经选拔后,决定从2名男生和2名女生中随机抽取2名学生参加比赛,求所抽取的学生中恰好是一男一女的概率.

答案:
(1)64.8 [解析]由题意,知其他垃圾所占的百分比为1-20%-7%-55%=18%,
∴其他垃圾所在的扇形的圆心角度数是360°×18%=64.8°;
(2)500×20%=100(吨),100×0.2=20(万元).故估计该天可回收物所创造的经济总价值是20万元;
(3)由题意,画树状图如图.
∴$P(\text{一男一女})=\frac{8}{12}=\frac{2}{3}$.
(1)64.8 [解析]由题意,知其他垃圾所占的百分比为1-20%-7%-55%=18%,
∴其他垃圾所在的扇形的圆心角度数是360°×18%=64.8°;
(2)500×20%=100(吨),100×0.2=20(万元).故估计该天可回收物所创造的经济总价值是20万元;
(3)由题意,画树状图如图.

∴$P(\text{一男一女})=\frac{8}{12}=\frac{2}{3}$.
9. 某市入选五一假期热门旅游城市.该市某景点为吸引游客,设置了一种游戏,其规则如下:凡参与游戏的游客从一个装有12个红球和若干个白球(每个球除颜色外,其他都相同)的不透明纸箱中,随机摸出一个球,摸到红球就可免费得到一个景点吉祥物.据统计参与这种游戏的游客共有60000人,景点一共为参与该游戏的游客免费发放了景点吉祥物15000个.
(1)求参与该游戏可免费得到景点吉祥物的频率.
(2)请你估计纸箱中白球的数量是多少?
(1)求参与该游戏可免费得到景点吉祥物的频率.
(2)请你估计纸箱中白球的数量是多少?
答案:
(1)参与该游戏可免费得到景点吉祥物的频率为$\frac{15000}{60000}=0.25$.
(2)设纸箱中白球的数量为x个,则可列方程$\frac{12}{12+x}=0.25$,解得x=36,经检验,x=36是分式方程的解,且符合实际.故估计纸箱中白球的数量是36个.
(1)参与该游戏可免费得到景点吉祥物的频率为$\frac{15000}{60000}=0.25$.
(2)设纸箱中白球的数量为x个,则可列方程$\frac{12}{12+x}=0.25$,解得x=36,经检验,x=36是分式方程的解,且符合实际.故估计纸箱中白球的数量是36个.
查看更多完整答案,请扫码查看


