第116页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
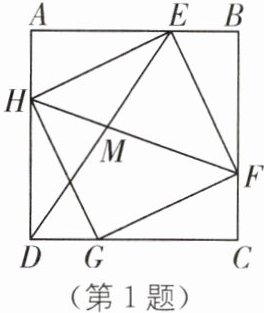
1.(2024·温州三模)如图,正方形ABCD由四个全等的直角三角形拼接而成,连结HF交DE于点M. 若$\frac{AH}{AE}= \frac{1}{2}$,则$\frac{HM}{MF}$的值为( ).
A.$\frac{4}{9}$
B.$\frac{1}{2}$
C.$\frac{4}{7}$
D.$\frac{2}{3}$

A.$\frac{4}{9}$
B.$\frac{1}{2}$
C.$\frac{4}{7}$
D.$\frac{2}{3}$
答案:
C [解析]如图所示,延长CB,DE交于点N,设AH=1,则AE=2,

∵正方形ABCD由四个全等的直角三角形拼接而成,
∴BE=1,DH=BF=2.
∵AD//BN,
∴△ADE∽△BNE,
∴$\frac{AD}{BN}$=$\frac{AE}{BE}$,即$\frac{3}{BN}$=$\frac{2}{1}$,
∴BN=1.5.
∵DH//NF,
∴△DHM∽△NFM,
∴$\frac{HM}{FM}$=$\frac{DH}{NF}$=$\frac{2}{3.5}$=$\frac{4}{7}$. 故选C.
C [解析]如图所示,延长CB,DE交于点N,设AH=1,则AE=2,

∵正方形ABCD由四个全等的直角三角形拼接而成,
∴BE=1,DH=BF=2.
∵AD//BN,
∴△ADE∽△BNE,
∴$\frac{AD}{BN}$=$\frac{AE}{BE}$,即$\frac{3}{BN}$=$\frac{2}{1}$,
∴BN=1.5.
∵DH//NF,
∴△DHM∽△NFM,
∴$\frac{HM}{FM}$=$\frac{DH}{NF}$=$\frac{2}{3.5}$=$\frac{4}{7}$. 故选C.
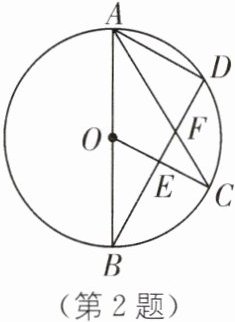
2.(2025·绍兴诸暨期末)如图,AB是$\odot O$的直径,D是$\odot O$上一点,连结AD和BD,C是$\widehat{BD}$的中点,连结OC和AC,分别交BD于点E和F.
(1)证明:$AD// OC$;
(2)若$BO= 5$,$BE= 4$,求DF的长.
(1)∵AB是⊙O的直径,
∴∠D=90°.
∵C是$\widehat{BD}$的中点,
∴OC垂直平分BD,
∴∠OEB=90°,
∴∠D=∠OEB,
∴AD//OC.
(2)∵AO=BO=CO=5,DE=BE=4,
∴AB=2AO=10,DB=2DE=8,
∴AD=$\sqrt{AB^2-DB^2}$=$\sqrt{10^2-8^2}$=6,
∴OE=$\frac{1}{2}$AD=3,
∴CE=CO - OE=5 - 3=2.
∵AD//CE,
∴△AFD∽△CFE,
∴$\frac{DF}{EF}$=$\frac{AD}{CE}$=$\frac{6}{2}$=3,
∴EF=$\frac{1}{3}$DF,
∴DF+$\frac{1}{3}$DF=4,
∴DF=3,
∴DF的长为3.
(1)证明:$AD// OC$;
(2)若$BO= 5$,$BE= 4$,求DF的长.

(1)∵AB是⊙O的直径,
∴∠D=90°.
∵C是$\widehat{BD}$的中点,
∴OC垂直平分BD,
∴∠OEB=90°,
∴∠D=∠OEB,
∴AD//OC.
(2)∵AO=BO=CO=5,DE=BE=4,
∴AB=2AO=10,DB=2DE=8,
∴AD=$\sqrt{AB^2-DB^2}$=$\sqrt{10^2-8^2}$=6,
∴OE=$\frac{1}{2}$AD=3,
∴CE=CO - OE=5 - 3=2.
∵AD//CE,
∴△AFD∽△CFE,
∴$\frac{DF}{EF}$=$\frac{AD}{CE}$=$\frac{6}{2}$=3,
∴EF=$\frac{1}{3}$DF,
∴DF+$\frac{1}{3}$DF=4,
∴DF=3,
∴DF的长为3.
答案:
(1)
∵AB是⊙O的直径,
∴∠D=90°.
∵C是$\widehat{BD}$的中点,
∴OC垂直平分BD,
∴∠OEB=90°,
∴∠D=∠OEB,
∴AD//OC.
(2)
∵AO=BO=CO=5,DE=BE=4,
∴AB=2AO=10,DB=2DE=8,
∴AD=$\sqrt{AB^2-DB^2}$=$\sqrt{10^2-8^2}$=6,
∴OE=$\frac{1}{2}$AD=3,
∴CE=CO - OE=5 - 3=2.
∵AD//CE,
∴△AFD∽△CFE,
∴$\frac{DF}{EF}$=$\frac{AD}{CE}$=$\frac{6}{2}$=3,
∴EF=$\frac{1}{3}$DF,
∴DF+$\frac{1}{3}$DF=4,
∴DF=3,
∴DF的长为3.
(1)
∵AB是⊙O的直径,
∴∠D=90°.
∵C是$\widehat{BD}$的中点,
∴OC垂直平分BD,
∴∠OEB=90°,
∴∠D=∠OEB,
∴AD//OC.
(2)
∵AO=BO=CO=5,DE=BE=4,
∴AB=2AO=10,DB=2DE=8,
∴AD=$\sqrt{AB^2-DB^2}$=$\sqrt{10^2-8^2}$=6,
∴OE=$\frac{1}{2}$AD=3,
∴CE=CO - OE=5 - 3=2.
∵AD//CE,
∴△AFD∽△CFE,
∴$\frac{DF}{EF}$=$\frac{AD}{CE}$=$\frac{6}{2}$=3,
∴EF=$\frac{1}{3}$DF,
∴DF+$\frac{1}{3}$DF=4,
∴DF=3,
∴DF的长为3.
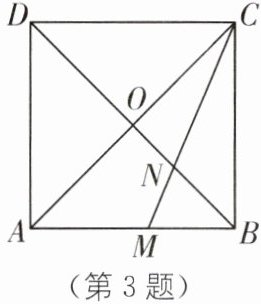
3. 如图,正方形ABCD的对角线AC与BD相交于点O,$\angle ACB$的平分线交AB,BD于M,N两点. 若$AM= 2$,则线段ON的长为( ).
A.$\frac{\sqrt{2}}{2}$
B.$\frac{\sqrt{3}}{2}$
C.1
D.$\frac{\sqrt{6}}{2}$

A.$\frac{\sqrt{2}}{2}$
B.$\frac{\sqrt{3}}{2}$
C.1
D.$\frac{\sqrt{6}}{2}$
答案:
C [解析]如图,过点M作MH⊥AC,垂足为H,
∴∠AHM=90°.
∵四边形ABCD为正方形,
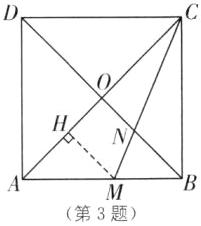
∴∠CAB=45°,AC⊥BD,
∴∠AMH=45°.
∴∠CAB=∠AMH,
∴AH=MH.
设正方形的边长为x,由AM=2,得BM=x - 2.
∵CM平分∠ACB,MH⊥AC,MB⊥BC,
∴BM=MH.
在Rt△AMH中,根据勾股定理,得$\sqrt{2}$(x - 2)=2,解得x=2+$\sqrt{2}$,则MH=AH=$\sqrt{2}$,OC=$\sqrt{2}$+1,AC=2$\sqrt{2}$+2,
∴CH=$\sqrt{2}$+2.
∵MH//ON,
∴△CON∽△CHM.
∴$\frac{CO}{CH}$=$\frac{ON}{MH}$,即$\frac{\sqrt{2}+1}{\sqrt{2}+2}$=$\frac{ON}{\sqrt{2}}$,解得ON=1. 故选C.
思路引导:熟悉常见的正方形模式图形、基本图形有利于将问题向熟悉的方向转化.
C [解析]如图,过点M作MH⊥AC,垂足为H,
∴∠AHM=90°.
∵四边形ABCD为正方形,

∴∠CAB=45°,AC⊥BD,
∴∠AMH=45°.
∴∠CAB=∠AMH,
∴AH=MH.
设正方形的边长为x,由AM=2,得BM=x - 2.
∵CM平分∠ACB,MH⊥AC,MB⊥BC,
∴BM=MH.
在Rt△AMH中,根据勾股定理,得$\sqrt{2}$(x - 2)=2,解得x=2+$\sqrt{2}$,则MH=AH=$\sqrt{2}$,OC=$\sqrt{2}$+1,AC=2$\sqrt{2}$+2,
∴CH=$\sqrt{2}$+2.
∵MH//ON,
∴△CON∽△CHM.
∴$\frac{CO}{CH}$=$\frac{ON}{MH}$,即$\frac{\sqrt{2}+1}{\sqrt{2}+2}$=$\frac{ON}{\sqrt{2}}$,解得ON=1. 故选C.
思路引导:熟悉常见的正方形模式图形、基本图形有利于将问题向熟悉的方向转化.
4.(2025·福建泉州洛江区期中改编)如图,在$\triangle ABC$中,点D,E,F分别在边AB,AC,BC上,连结DE,DF,BE,DF与BE交于点G. 已知四边形DFCE是平行四边形,且$\frac{DE}{BC}= \frac{2}{5}$. 若$AC= 25$,求线段AE,GF的长.
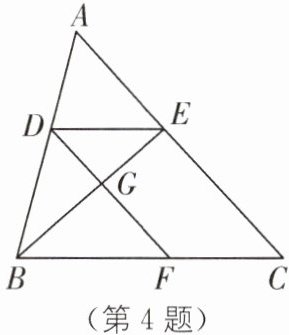

答案:
∵四边形DFCE是平行四边形,
∴DE//BC,DF//AC,DE=CF,
∴△ADE∽△ABC,
∴$\frac{AE}{AC}$=$\frac{DE}{BC}$=$\frac{2}{5}$.
∵AC=25,
∴AE=10,
∴CE=25 - 10=15.
∵$\frac{DE}{BC}$=$\frac{CF}{BC}$=$\frac{2}{5}$,
∴$\frac{BF}{BC}$=$\frac{3}{5}$.
∵DF//AC,
∴△BFG∽△BCE,
∴$\frac{GF}{CE}$=$\frac{BF}{BC}$=$\frac{3}{5}$,
∴GF=9.
∵四边形DFCE是平行四边形,
∴DE//BC,DF//AC,DE=CF,
∴△ADE∽△ABC,
∴$\frac{AE}{AC}$=$\frac{DE}{BC}$=$\frac{2}{5}$.
∵AC=25,
∴AE=10,
∴CE=25 - 10=15.
∵$\frac{DE}{BC}$=$\frac{CF}{BC}$=$\frac{2}{5}$,
∴$\frac{BF}{BC}$=$\frac{3}{5}$.
∵DF//AC,
∴△BFG∽△BCE,
∴$\frac{GF}{CE}$=$\frac{BF}{BC}$=$\frac{3}{5}$,
∴GF=9.
5. 如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且$CF= 3FD$,$\angle BEF= 90^\circ$.
(1)求证:$\triangle ABE\backsim\triangle DEF$;
(2)若$AB= 4$,延长EF交BC的延长线于点G,求BG的长.
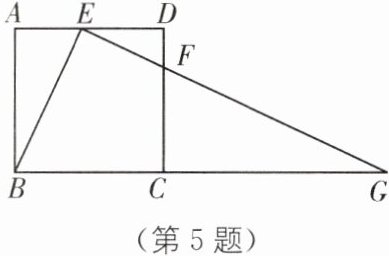
(1)求证:$\triangle ABE\backsim\triangle DEF$;
(2)若$AB= 4$,延长EF交BC的延长线于点G,求BG的长.

答案:
(1)
∵四边形ABCD为正方形,
∴∠A=∠D=90°,
∴∠ABE+∠AEB=90°.
∵∠BEF=90°,
∴∠AEB+∠DEF=90°,
∴∠ABE=∠DEF,
∴△ABE∽△DEF.
(2)
∵AB=BC=CD=AD=4,CF=3FD,E为边AD的中点,
∴DF=1,CF=3,DE=2.
∵ED//CG,
∴△EDF∽△GCF,
∴$\frac{ED}{CG}$=$\frac{DF}{CF}$,
∴$\frac{2}{CG}$=$\frac{1}{3}$,解得CG=6.
∴BG=BC+CG=10.
(1)
∵四边形ABCD为正方形,
∴∠A=∠D=90°,
∴∠ABE+∠AEB=90°.
∵∠BEF=90°,
∴∠AEB+∠DEF=90°,
∴∠ABE=∠DEF,
∴△ABE∽△DEF.
(2)
∵AB=BC=CD=AD=4,CF=3FD,E为边AD的中点,
∴DF=1,CF=3,DE=2.
∵ED//CG,
∴△EDF∽△GCF,
∴$\frac{ED}{CG}$=$\frac{DF}{CF}$,
∴$\frac{2}{CG}$=$\frac{1}{3}$,解得CG=6.
∴BG=BC+CG=10.
查看更多完整答案,请扫码查看


