《2025年实验班提优训练九年级数学上册浙教版》

9. 中考新考法 满足条件的结论开放 (2025·河南洛阳老城区期中)第二十四届北京冬奥会入场式引导牌上的图案融入了中国结和雪花两种元素.如图,这个图案绕着它的中心旋转角$\alpha(0^{\circ }＜\alpha ＜360^{\circ })$后能够与它本身重合,则角$\alpha$可以为60度.(写出一个即可)

答案： 60(答案不唯一)　[解析]360°÷6=60°,则这个图案绕着它的中心旋转60°后能够与它本身重合.

10. (2025·安徽阜阳期中改编)如图,直线$a// b,\triangle AOB$的边 OB 在直线 b 上,$\angle AOB= 55^{\circ }$,将$\triangle AOB$绕点 O 顺时针旋转$75^{\circ }至\triangle A_{1}OB_{1}$,边$A_{1}O$交直线 a 于点 C,则$\angle 1= $______°.

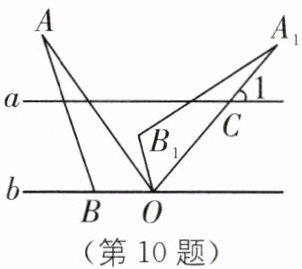
答案：
50　[解析]如图，
∵将△AOB绕点O顺时针旋转75°至△A₁OB₁,

∴∠A₁OB₁=∠AOB=55°,∠AOA₁=75°,
∴∠2=180°−55°−75°=50°.
∵直线a//b,
∴∠1=∠2=50°.

11. (2025·重庆江津中学期中)如图,在正方形 ABCD 中,将边 BC 绕点 B 逆时针旋转至$BC'$,连结$CC',DC'$,若$\angle CC'D= 90^{\circ },C'D= 3$,则正方形 ABCD 的边长为______.

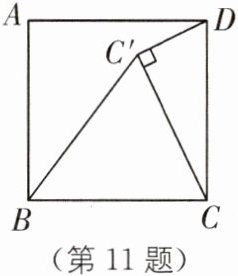
答案：
3$\sqrt{5}$　[解析]如图，过点B作BE⊥CC'于点E.

∵四边形ABCD是正方形，
∴BC=CD,∠BCD=90°,
∴∠BCE+∠C'CD=90°.
∵∠BCE+∠CBE=90°,
∴∠C'CD=∠CBE.
又∠BEC=∠CC'D=90°,
∴△BCE≌△CDC',
∴CE=C'D=3.
∵将边BC绕点B逆时针旋转至BC',
∴BC=BC'.
又BE⊥CC',
∴CE=C'E=C'D=3,
∴CC'=6,
∴CD = $\sqrt{C'D^{2}+C'C^{2}}$ = $\sqrt{3^{2}+6^{2}}$ = 3$\sqrt{5}$.
∴正方形ABCD的边长为3$\sqrt{5}$.

12. 手拉手模型 (2025·绍兴诸暨期中)如图,在矩形 ABCD 中,$BC= 2AB$,点 P 为边 AD 上的一个动点,线段 BP 绕点 B 顺时针旋转$60^{\circ }得到线段BP'$,连结$PP',CP'$.当点$P'$落在边 BC 上时,$\angle PP'C$的度数为______,当线段$CP'$的长度最小时,$\angle PP'C$的度数为______.

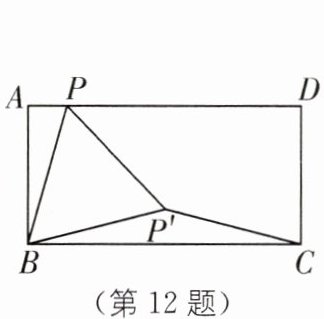
答案：
120°　75°　[解析]当点P'落在边BC上时，如图
(1).

由题可得△BPP'是等边三角形，
∴∠PP'B=60°,
∴∠PP'C=180°−∠PP'B=180°−60°=120°.
如图
(2)，以AB为边向右作等边三角形ABE，连结EP'.

∵△BPP'是等边三角形,
∴∠ABE=∠PBP'=60°,BP=BP',BA=BE,
∴∠ABP=∠EBP'.
在△ABP和△EBP'中，{BA=BE,∠ABP=∠EBP',BP=BP'},
∴△ABP≌△EBP'(SAS).
∴∠BAP=∠BEP'=90°.
∴点P'在射线EP'上运动.
如图
(3)，设EP'交BC于点O,

当点P'落在BC上时，点P'与O重合，此时∠PP'C=180°−60°=120°,
当CP'⊥EP'时，CP'的长度最小，此时∠EBO=∠OCP'=30°,
∴EO=$\frac{1}{2}$OB,OP'=$\frac{1}{2}$OC,
∴EP'=EO+OP'=$\frac{1}{2}$OB+$\frac{1}{2}$OC=$\frac{1}{2}$BC.
∵BC=2AB,
∴EP'=AB=EB,
∴∠EBP'=∠EP'B=45°,
∴∠BP'C=45°+90°=135°,
∴∠PP'C=∠BP'C−∠BP'P=135°−60°=75°.

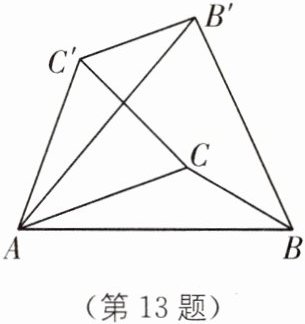
13. 如图,在$\triangle ABC$中,$\angle CAB= 20^{\circ },\angle ABC= 30^{\circ }$,将$\triangle ABC$绕点 A 逆时针旋转$50^{\circ }得到\triangle AB'C'$,以下结论:①$BC= B'C'$;②$AC// C'B'$;③$C'B'\perp BB'$;④$\angle ABB'= \angle ACC'$.其中正确的结论是______①②④.

答案： ①②④　[解析]①
∵△ABC绕点A逆时针旋转50°得到△AB'C'，
∴BC=B'C'.故①正确;
②
∵△ABC绕点A逆时针旋转50°得到△AB'C'，
∴∠BAB'=50°.
∵∠CAB=20°,
∴∠B'AC=∠BAB'−∠CAB=30°.
∵∠AB'C'=∠ABC=30°,
∴∠AB'C'=∠B'AC,
∴AC//C'B'.故②正确;
③在△BAB'中，AB=AB'，∠BAB'=50°,
∴∠AB'B=∠ABB'=$\frac{1}{2}$×(180°−50°)=65°,
∴∠BB'C'=∠AB'B+∠AB'C'=65°+30°=95°,
∴C'B'与BB'不垂直.故③错误;
④在△ACC'中，AC=AC'，∠CAC'=50°,
∴∠ACC'=$\frac{1}{2}$×(180°−50°)=65°,
∴∠ABB'=∠ACC'.故④正确.
∴①②④这三个结论正确.
归纳总结　本题考查了旋转性质的应用，图形的旋转只改变图形的位置，不改变图形的形状与大小.

14. (2025·河北沧州期末)一副三角板按图(1)放置,O 是边 BC(DF)的中点,$BC= 12cm$,如图(2),将$\triangle ABC$绕点 O 顺时针旋转$60^{\circ }$,AC 与 EF 相交于点 G,则 FG 的长是______cm.

答案：
(3$\sqrt{3}$ - 3)　[解析]如图，设EF与BC交于点H,

∵O是边BC(DF)的中点，BC=12cm,
∴OD=OF=OB=OC=6cm.
∵将△ABC绕点O顺时针旋转60°,
∴∠BOD=∠FOH=60°.
∵∠F=30°,
∴∠FHO=90°,
∴OH=$\frac{1}{2}$OF=3cm,
∴FH = $\sqrt{OF^{2}-OH^{2}}$ = 3$\sqrt{3}$cm,
∴CH=OC−OH=3cm.
∵∠C=45°,
∴GH=CH=3cm,
∴FG=FH−GH=(3$\sqrt{3}$ - 3)cm.

15. 如图,菱形 ABCD 中对角线 AC 与 BD 相交于点 F,且$AC= 8,BD= 8\sqrt {3}$,若点 P 是对角线 BD 上一动点,连结 AP,将 AP 绕点 A 逆时针旋转至 AE,使得$\angle PAE= \angle BAD$,连结 PE,取 AD 的中点 O,连结 OE,则在点 P 的运动过程中,求线段 OE 的最小值.

答案：
如图，连结ED.

∵四边形ABCD是菱形，且AC=8,BD=8$\sqrt{3}$,
∴AF=$\frac{1}{2}$AC=4,DF=$\frac{1}{2}$BD=4$\sqrt{3}$,AC⊥BD,BA=DA,
∴AD = $\sqrt{AF^{2}+DF^{2}}$ = $\sqrt{4^{2}+(4\sqrt{3})^{2}}$ = 8,
∴∠ADB=∠ABD=30°.
将AP绕点A逆时针旋转至AE，使得∠PAE=∠BAD,
∴PA=EA,∠BAP=∠DAE.
在△BAP和△DAE中，{BA=DA,∠BAP=∠DAE,PA=EA},
∴△BAP≌△DAE(SAS),
∴∠ADE=∠ABP=30°,
∴DE是满足∠ADE=30°的线段,
当OE⊥DE时，OE的值最小.
∵O是AD的中点，
∴OD=$\frac{1}{2}$AD=$\frac{1}{2}$×8=4,
∴OE=$\frac{1}{2}$OD=$\frac{1}{2}$×4=2,
∴在点P的运动过程中，线段OE的最小值为2.