第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
4.(2024·江西抚州临川区期中)在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)用树状图或列表法表示出$(x,y)$的所有可能出现的结果;
(2)求小明、小华各取一次小球所确定的点$(x,y)落在反比例函数y= \frac{4}{x}$的图象上的概率.
(1)用树状图或列表法表示出$(x,y)$的所有可能出现的结果;
(2)求小明、小华各取一次小球所确定的点$(x,y)落在反比例函数y= \frac{4}{x}$的图象上的概率.
答案:
4.
(1)列表如下:

(2)共有16种等可能的结果,其中落在$y=\frac{4}{x}$图象上的结果有3种,
∴$P=\frac{3}{16}$。
4.
(1)列表如下:

(2)共有16种等可能的结果,其中落在$y=\frac{4}{x}$图象上的结果有3种,
∴$P=\frac{3}{16}$。
5. 在3张相同的小纸条上,分别写上条件:①四边形ABCD是菱形;②四边形ABCD有一个内角是直角;③四边形ABCD的对角线相等.将这3张小纸条做成3支签,放在一个不透明的盒子中.
(1)搅匀后从中任意抽出1支签,抽到条件①的概率是______;
(2)搅匀后先从中任意抽出1支签(不放回),再从余下的2支签中任意抽出1支签.四边形ABCD同时满足抽到的2张小纸条上的条件,求四边形ABCD一定是正方形的概率.
(1)搅匀后从中任意抽出1支签,抽到条件①的概率是______;
(2)搅匀后先从中任意抽出1支签(不放回),再从余下的2支签中任意抽出1支签.四边形ABCD同时满足抽到的2张小纸条上的条件,求四边形ABCD一定是正方形的概率.
答案:
5.
(1)$\frac{1}{3}$
(2)画树状图如图。
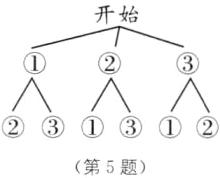
共有6种等可能的结果,当两次抽到的结果为①②或①③时,四边形ABCD一定是正方形,
∴所求的结果有4种,故四边形ABCD一定是正方形的概率为$\frac{4}{6}=\frac{2}{3}$。
5.
(1)$\frac{1}{3}$
(2)画树状图如图。

共有6种等可能的结果,当两次抽到的结果为①②或①③时,四边形ABCD一定是正方形,
∴所求的结果有4种,故四边形ABCD一定是正方形的概率为$\frac{4}{6}=\frac{2}{3}$。
6.(2024·杭州拱墅区期末)一个质地均匀的木质正四面体,四个面上分别刻有1到4的点数.
(1)投掷一次,求底面的点数是偶数的概率$P_1$;
(2)投掷两次,求两次底面的点数之和是偶数的概率$P_2$(用树状图或列表法).
(1)投掷一次,求底面的点数是偶数的概率$P_1$;
(2)投掷两次,求两次底面的点数之和是偶数的概率$P_2$(用树状图或列表法).
答案:
6.
(1)投掷一次,共有4种等可能的结果,其中底面的点数是偶数的结果有2种,故底面的点数是偶数的概率$P_1$为$\frac{2}{4}=\frac{1}{2}$。
(2)列表如下:

由表,知共有16种等可能结果,其中两次底面的点数之和是偶数的结果有8种,所以两次底面的点数之和是偶数的概率$P_2$为$\frac{8}{16}=\frac{1}{2}$。
6.
(1)投掷一次,共有4种等可能的结果,其中底面的点数是偶数的结果有2种,故底面的点数是偶数的概率$P_1$为$\frac{2}{4}=\frac{1}{2}$。
(2)列表如下:

由表,知共有16种等可能结果,其中两次底面的点数之和是偶数的结果有8种,所以两次底面的点数之和是偶数的概率$P_2$为$\frac{8}{16}=\frac{1}{2}$。
7.(2024·杭州拱墅区三模)某停车场现仅剩下“C001”“C002”“C003”“C004”四个车位.
(1)若有一辆小汽车停车,则这辆车停在“C002”号车位的概率是______;
(2)分别记这四个车位为A,B,C,D,小明和小红同时来到该处停车,用画树状图或列表的方法,求两人停车在相邻车位的概率.
(1)若有一辆小汽车停车,则这辆车停在“C002”号车位的概率是______;
(2)分别记这四个车位为A,B,C,D,小明和小红同时来到该处停车,用画树状图或列表的方法,求两人停车在相邻车位的概率.
答案:
7.
(1)$\frac{1}{4}$ [解析]
∵现仅剩下"C001""C002""C003""C004"四个车位,
∴有一辆小汽车停车,则这辆车停在"C002"号车位的概率是$\frac{1}{4}$。
(2)由题意,画树状图如图。

共有12种等可能的结果,其中小明和小红两人停在相邻车位的结果有6种,
∴两人停在相邻车位的概率为$\frac{6}{12}=\frac{1}{2}$。
7.
(1)$\frac{1}{4}$ [解析]
∵现仅剩下"C001""C002""C003""C004"四个车位,
∴有一辆小汽车停车,则这辆车停在"C002"号车位的概率是$\frac{1}{4}$。
(2)由题意,画树状图如图。

共有12种等可能的结果,其中小明和小红两人停在相邻车位的结果有6种,
∴两人停在相邻车位的概率为$\frac{6}{12}=\frac{1}{2}$。
8. 如图,在$3×3$的正方形网格中,点A,B,C,D,E,F都是格点.
(1)从A,D,E,F四点中任意取一点,以这点及点B,C为顶点画三角形,求所画三角形是等腰三角形的概率; (2)从A,D,E,F四点中任意取两点,以这两点及点B,C为顶点画四边形,求所画四边形
是平行四边形的概率.
(1)从A,D,E,F四点中任意取一点,以这点及点B,C为顶点画三角形,求所画三角形是等腰三角形的概率; (2)从A,D,E,F四点中任意取两点,以这两点及点B,C为顶点画四边形,求所画四边形

是平行四边形的概率.
答案:
8.
(1)
∵从A,D,E,F四个点中任意取一点,一共有4种等可能的结果,只有选取点D时,所画三角形是等腰三角形,
∴P(所画三角形是等腰三角形)$=\frac{1}{4}$。故所画三角形是等腰三角形的概率为$\frac{1}{4}$。
(2)画树状图如图。

共有12种等可能的结果。
∵以点A,E,B,C为顶点及以D,F,B,C为顶点所画的四边形是平行四边形,
∴所画的四边形是平行四边形的概率$P=\frac{4}{12}=\frac{1}{3}$。
8.
(1)
∵从A,D,E,F四个点中任意取一点,一共有4种等可能的结果,只有选取点D时,所画三角形是等腰三角形,
∴P(所画三角形是等腰三角形)$=\frac{1}{4}$。故所画三角形是等腰三角形的概率为$\frac{1}{4}$。
(2)画树状图如图。

共有12种等可能的结果。
∵以点A,E,B,C为顶点及以D,F,B,C为顶点所画的四边形是平行四边形,
∴所画的四边形是平行四边形的概率$P=\frac{4}{12}=\frac{1}{3}$。
查看更多完整答案,请扫码查看


