《2025年实验班提优训练九年级数学上册浙教版》

1. 教材 P100 作业题 T4·变式 (2025·绍兴柯桥区期末)如图,已知正五边形 ABCDE 内接于$\odot O$,连结 OB,BD,则$∠OBD$的度数是( ).

A.$17^{\circ }$
B.$18^{\circ }$
C.$19^{\circ }$
D.$20^{\circ }$
]

答案：
B　[解析]如图，连结OC.
∵五边形ABCDE是$\odot O$的内接正五边形，
∴$∠BOC=\frac {360^{\circ }}{5}=72^{\circ },$
　　　　　　　　　　　　　　　　
∴$∠BDC=\frac {1}{2}∠BOC=36^{\circ }.$
∵$OB=OC,BC=CD,$
∴$∠OBC=∠OCB=\frac {180^{\circ }-72^{\circ }}{2}=54^{\circ },∠DBC=∠BDC=36^{\circ },$
∴$∠OBD=54^{\circ }-36^{\circ }=18^{\circ }.$
故选B.
知识拓展　正多边形的有关概念:
①中心:正多边形的外接圆的圆心叫做正多边形的中心.
②正多边形的半径:外接圆的半径叫做正多边形的半径.
③中心角:正多边形每一边所对的圆心角叫做正多边形的中心角.
④边心距:中心到正多边形的一边的距离叫做正多边形的边心距.

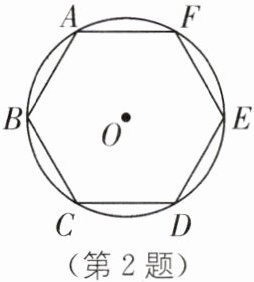
2.(2025·四川绵阳期末)如图,正六边形 ABCDEF 内接于$\odot O$,若$\odot O的周长是6π$,则正六边形的边长是( ).

A.$\sqrt {3}$
B.3
C.6
D.$2\sqrt {3}$

答案：
B　[解析]连结OD,OC,如图.
∵$\odot O$的周长等于$6π,$
∴$\odot O$的半径$OD=OC=\frac {6π}{2π}=3.$
　　　　　　　　　　　　　　　　
∵六边形ABCDEF是正六边形，
∴$∠DOC=\frac {360^{\circ }}{6}=60^{\circ },$
∴$△DOC$是等边三角形，
∴$DC=OD=OC=3$,即正六边形的边长为3.
故选B.

3. 如图,小陈从 O 点出发,前进 6 米后向右转$20^{\circ }$,再前进 6 米后又向右转$20^{\circ },...$,这样一直走下去,他第一次回到出发点 O 时一共走了 108 米.

答案： 108　[解析]依题意可知，小陈所走路径为正多边形，设这个正多边形的边数为n，
则$20n=360$，解得$n=18$，
∴他第一次回到出发点O时一共走了$6×18=108$(米).

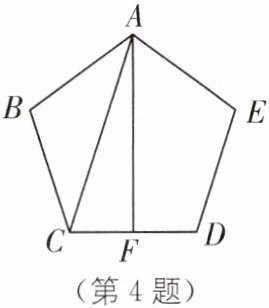
4. 如图,在正五边形 ABCDE 中,F 为 CD 边中点,连结 AF,CA,求$∠CAF$的度数.
]

答案：
如图，连结AD.
∵五边形ABCDE为正五边形，
∴$AB=AE=BC=DE,$
$∠B=∠E.$
　　　　　　　　　　　　　　　　
在$△ABC$与$△AED$中，
$\begin{cases}AB = AE\\∠B = ∠E\\BC = ED\end{cases}$
∴$△ABC\cong △AED(SAS),$
∴$∠BAC=∠EAD,AC=AD.$
∵F为CD边中点，$AF⊥CD$，
∴$∠AFC=90^{\circ }.$
∵五边形ABCDE是正五边形，
∴$∠B=∠BCD=\frac {(5 - 2)×180^{\circ }}{5}=108^{\circ },BA=BC,$
∴$∠BCA=∠BAC=\frac {180^{\circ }-108^{\circ }}{2}=36^{\circ },$
∴$∠ACF=∠BCD - ∠BCA=72^{\circ },$
∴$∠CAF=90^{\circ }-∠ACF=18^{\circ }.$

5.(2024·杭州萧山区八校联考)一个圆的内接正六边形与内接正方形的边长之比为(C).
A.$3:2$
B.$1:\sqrt {3}$
C.$1:\sqrt {2}$
D.$\sqrt {2}:\sqrt {3}$

答案： C　[解析]设此圆的半径为R，
它的内接正六边形的边长为R，
它的内接正方形的边长为$\sqrt {2}R$，
故一个圆的内接正六边形和内接正方形的边长比为$R:\sqrt {2}R = 1:\sqrt {2}$.
故选C.

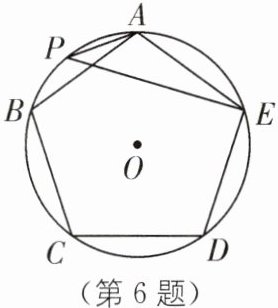
6.(2024·天津南开区期末)如图,正五边形 ABCDE 内接于$\odot O$,P 为$\widehat {AB}$上一点,连结 PA,PE,则$∠APE$的度数为( ).

A.$18^{\circ }$
B.$36^{\circ }$
C.$54^{\circ }$
D.$72^{\circ }$
]

答案：
B　[解析]如图，连结OA,OE,
∵正五边形ABCDE内接于$\odot O$，
∴$∠AOE=\frac {1}{5}×360^{\circ }=72^{\circ }.$
　　　　　　　　　　　　　　　　
∵P为$\widehat {AB}$上一点，
∴$∠APE=\frac {1}{2}∠AOE=\frac {1}{2}×72^{\circ }=36^{\circ }.$
故选B.

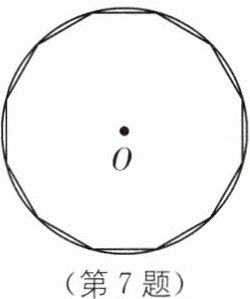
7. 数形结合思想 (2025·山东聊城期末)刘徽在《九章算术注》中首创“割圆术”,利用圆的内接正多边形来确定圆周率,开创了中国数学发展史上圆周率研究的新纪元.某同学在学习“割圆术”的过程中,作了一个如图所示的圆内接正十二边形.若$\odot O$的半径为 2,则这个圆内接正十二边形的面积为( )

A.3
B.12
C.$4π$
D.$12π$

答案：
B　[解析]通过“割圆术”作了一个如图所示的圆内接正十二边形，如图，过A作$AC⊥OB$于C，
　　　　　　　　　
∵圆的内接正十二边形的圆心角为$\frac {360^{\circ }}{12}=30^{\circ },OA = 2,$
∴$AC=\frac {1}{2}OA=1,$
∴$S_{\triangle OAB}=\frac {1}{2}×2×1 = 1,$
∴这个圆的内接正十二边形的面积为$12×1 = 12,$
故选B.

8.(2025·杭州西湖区期末)如图,已知正方形 ABCD 与正五边形 EFGCH 都内接于$\odot O$,则$∠DCH$的度数为$9^{\circ }$.

答案： $9^{\circ }$　[解析]
∵正方形ABCD与正五边形EFGCH都内接于$\odot O$，
∴$CH = CG,CD = CB,$
∴$\widehat {CH}=\widehat {CG},\widehat {CD}=\widehat {CB},$
∴$\widehat {DH}=\widehat {BG},$
∴$∠DCH=∠BCG.$
∵$∠HCG=\frac {(5 - 2)×180^{\circ }}{5}=108^{\circ },∠DCB = 90^{\circ },$
∴$∠DCH=∠BCG=\frac {1}{2}×\frac {∠HCG - ∠DCB}{2}=\frac {108^{\circ }-90^{\circ }}{2}=9^{\circ }.$

9.(2024·上海闵行区三模)蜂巢结构精巧,其巢房横截面的形状均为正六边形.如图是部分巢房的横截面图,图中7个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点 P,Q,M 均为正六边形的顶点.若点 P,Q 的坐标分别为$(-2\sqrt {3},3),(0,-3)$,则点 M 的坐标为 _ .

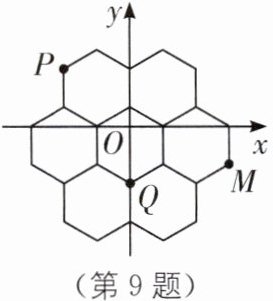
答案：
$(3\sqrt {3},-2)$　[解析]如图，设中间正六边形的中心为D，连结DB.
∵点P，Q的坐标分别为$(-2\sqrt {3},3),(0,-3),$
图中是7个全等的正六边形，
　　　　　　　　　　　　　　　　
∴$AB = BC = 2\sqrt {3},OQ = 3,$
∴$OA = OB=\sqrt {3},$
∴$OC = 3\sqrt {3}.$
∵$DQ = DB = 2OD,$
∴$OD = 1,QD = DB = CM = 2,$
∴$M(3\sqrt {3},-2).$