第104页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
9.(2025·福建泉州鲤城区期中)商家通常依据"乐观系数准则"确定商品销售价格,即根据商品的最低销售限价a、最高销售限价b(b>a)以及实数x(0<x<1)确定实际销售价格c= a+x(b-a),这里,x被称为乐观系数.经验表明,最佳乐观系数x恰好使得(b-a)/(c-a)= (c-a)/(b-c),据此可得,最佳乐观系数x的值等于
(√5-1)/2
.
答案:
9.(√5-1)/2 解析
∵c-a=x(b-a),b-c=(b-a)-x(b-a),b-a/c-a=c-a/b-c,
∴[x(b-a)]²=(b-a)²-x(b-a)²,
∴x²+x-1=0,解得x=(-1±√5)/2.
∵0<x<1,
∴x=(√5-1)/2.
∵c-a=x(b-a),b-c=(b-a)-x(b-a),b-a/c-a=c-a/b-c,
∴[x(b-a)]²=(b-a)²-x(b-a)²,
∴x²+x-1=0,解得x=(-1±√5)/2.
∵0<x<1,
∴x=(√5-1)/2.
10. 传统文化 二胡 (2024·济南槐荫区二模)二胡是中国古老的民族拉弦乐器之一,演奏家发现,二胡的"千斤"钩在琴弦长的黄金分割点处("千斤"上面一截琴弦比下面一截琴弦短),奏出来的音调最和谐悦耳.如图,一把二胡的琴弦长为80 cm,求"千斤"下面一截琴弦长(结果保留根号).


答案:
10.
∵二胡的“千斤”钩在琴弦长的黄金分割点处,且“千斤”上面一截琴弦比下面一截琴弦短,则令“千斤”下面一截琴弦长为x cm,
∴x/80=(√5-1)/2,解得x=40√5-40,
∴“千斤”下面一截琴弦长为(40√5-40)cm.
∵二胡的“千斤”钩在琴弦长的黄金分割点处,且“千斤”上面一截琴弦比下面一截琴弦短,则令“千斤”下面一截琴弦长为x cm,
∴x/80=(√5-1)/2,解得x=40√5-40,
∴“千斤”下面一截琴弦长为(40√5-40)cm.
11. 中考新考法 新定义问题 (2025·山西临汾期中)阅读理解:二次根式的除法,要化去分母中的根号,需将分子、分母同乘一个恰当的二次根式.
例如:化简1/(√3-√2).
解:将分子、分母同乘√3+√2,得1/(√3-√2)= (√3+√2)/[(√3-√2)(√3+√2)]= √3+√2.
拓展延伸:
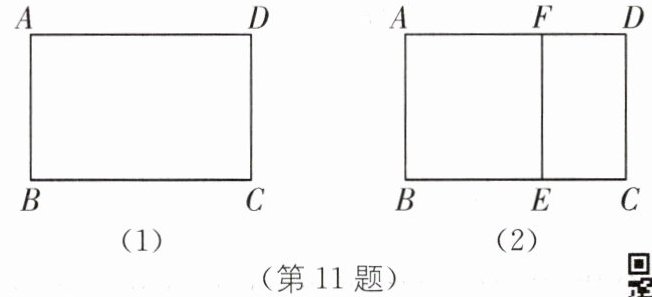
宽与长的比是(√5-1)/2的矩形叫黄金矩形.如图(1),已知黄金矩形ABCD的宽AB= √2.
(1)求黄金矩形ABCD中BC边的长;
(2)如图(2),将图(1)中的黄金矩形裁剪掉一个以AB为边的正方形ABEF,得到新的矩形DCEF,猜想矩形DCEF是否为黄金矩形,并证明你的结论.
例如:化简1/(√3-√2).
解:将分子、分母同乘√3+√2,得1/(√3-√2)= (√3+√2)/[(√3-√2)(√3+√2)]= √3+√2.
拓展延伸:
宽与长的比是(√5-1)/2的矩形叫黄金矩形.如图(1),已知黄金矩形ABCD的宽AB= √2.
(1)求黄金矩形ABCD中BC边的长;
(2)如图(2),将图(1)中的黄金矩形裁剪掉一个以AB为边的正方形ABEF,得到新的矩形DCEF,猜想矩形DCEF是否为黄金矩形,并证明你的结论.

答案:
11.
(1)
∵宽与长的比是(√5-1)/2的矩形叫黄金矩形,黄金矩形ABCD的宽AB=√2,
∴AB/BC=(√5-1)/2=√2/BC,
∴BC=2√2/(√5-1)=[2√2(√5+1)]/[(√5-1)(√5+1)]=(√10+√2)/2.
(2)矩形DCEF是黄金矩形.理由如下:
∵黄金矩形裁剪掉一个以AB为边的正方形ABEF,得到新的矩形DCEF,
∴BE=AB=CD=√2,EC=BC-BE=(√10+√2)/2-√2=(√10-√2)/2,
∴EC/CD=(√10-√2)/(2√2)=[√2(√5-1)]/(2√2)=(√5-1)/2,故矩形DCEF是黄金矩形.
(1)
∵宽与长的比是(√5-1)/2的矩形叫黄金矩形,黄金矩形ABCD的宽AB=√2,
∴AB/BC=(√5-1)/2=√2/BC,
∴BC=2√2/(√5-1)=[2√2(√5+1)]/[(√5-1)(√5+1)]=(√10+√2)/2.
(2)矩形DCEF是黄金矩形.理由如下:
∵黄金矩形裁剪掉一个以AB为边的正方形ABEF,得到新的矩形DCEF,
∴BE=AB=CD=√2,EC=BC-BE=(√10+√2)/2-√2=(√10-√2)/2,
∴EC/CD=(√10-√2)/(2√2)=[√2(√5-1)]/(2√2)=(√5-1)/2,故矩形DCEF是黄金矩形.
12. 传统文化 汉字字形 (2024·山西中考)黄金分割是汉字结构最基本的规律.借助如图的正方形习字格书写的汉字"晋"端庄稳重、舒展美观.已知一条分割线的端点A,B分别在习字格的边MN,PQ上,且AB//NP,"晋"字的笔画"、"的位置在AB的黄金分割点C处,且BC/AB= (√5-1)/2,若NP= 2 cm,则BC的长为
√5-1
cm(结果保留根号).
答案:
12.(√5-1) 解析
∵四边形MNPQ是正方形,
∴∠N=∠P=90°.又AB//NP,
∴∠BAN+∠N=180°,
∴∠BAN=90°,
∴四边形ABPN是矩形,
∴AB=NP=2 cm.又BC/AB=(√5-1)/2,
∴BC=(√5-1)cm.
∵四边形MNPQ是正方形,
∴∠N=∠P=90°.又AB//NP,
∴∠BAN+∠N=180°,
∴∠BAN=90°,
∴四边形ABPN是矩形,
∴AB=NP=2 cm.又BC/AB=(√5-1)/2,
∴BC=(√5-1)cm.
查看更多完整答案,请扫码查看


