第56页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
1.(2024·丽水期末)$\odot O$的半径为5 cm,点A在$\odot O$外,则AO的长可以是(
A.3 cm
B.4 cm
C.5 cm
D.6 cm
D
).A.3 cm
B.4 cm
C.5 cm
D.6 cm
答案:
D
2. 教材P68作业题T5·变式 (2024·台州温岭期末)已知$\odot O$的半径为6,点A与点O的距离为5,则点A与$\odot O$的位置关系是(
A.点A在圆外
B.点A在圆内
C.点A在圆上
D.不确定
B
).A.点A在圆外
B.点A在圆内
C.点A在圆上
D.不确定
答案:
B [解析]
∵⊙O的半径为6,点A到圆心O的距离为5,5<6,
∴点A在圆内.故选B.
∵⊙O的半径为6,点A到圆心O的距离为5,5<6,
∴点A在圆内.故选B.
3. 已知$\odot O$半径为r,点P为$\odot O$内一点,$OP= 6$,则r满足的条件是(
A.$r= 6$
B.$r>6$
C.$0<r<6$
D.$r≠6$
B
).A.$r= 6$
B.$r>6$
C.$0<r<6$
D.$r≠6$
答案:
B [解析]
∵点P为⊙O内一点,OP=6,
∴r>6.故选B.
∵点P为⊙O内一点,OP=6,
∴r>6.故选B.
4. 传统文化 《墨经》 战国时的《墨经》就有“圆,一中同长也”的记载. 它的大致意思是圆有一个圆心,圆上各点到圆心的距离都等于半径. 如图,在$\odot O$中:
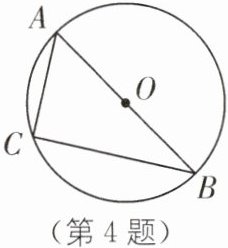
(1)直径有
(2)半径有
(3)弦有
(4)劣弧有
(5)优弧有

(1)直径有
线段AB
;(2)半径有
线段OA,OB
;(3)弦有
线段AC,CB,AB
;(4)劣弧有
$\overset{\frown}{AC}$,$\overset{\frown}{CB}$
;(5)优弧有
∠CAB,∠ABC
.
答案:
(1)线段AB
(2)线段OA,OB
(3)线段AC,CB,AB
(4)$\overset{\frown}{AC}$,$\overset{\frown}{CB}$
(5)∠CAB,∠ABC
(1)线段AB
(2)线段OA,OB
(3)线段AC,CB,AB
(4)$\overset{\frown}{AC}$,$\overset{\frown}{CB}$
(5)∠CAB,∠ABC
5. 如图,在$\triangle ABC$中,$AC= 4$,$BC= 3$,$\angle C= 90^\circ$,以点C为圆心作$\odot C$,半径为r.
(1)当r在什么范围时,点A,B在$\odot C$外?
(2)当r在什么范围时,点B在$\odot C$内,点A在$\odot C$外?
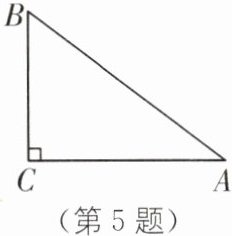
(1)当r在什么范围时,点A,B在$\odot C$外?
(2)当r在什么范围时,点B在$\odot C$内,点A在$\odot C$外?

答案:
(1)0<r<3.
(2)3<r<4.
(1)0<r<3.
(2)3<r<4.
6. 新情境 雷达监测 (2024·湖州期末)雷达通过无线电的方法发现目标并测定它们的空间位置,现有一款监测半径为5 km的雷达,监测点的分布情况如图,如果将雷达装置设在点P,每一个小方格的边长为1 km,那么M,N,O,Q四个点中能被雷达监测到的点有(
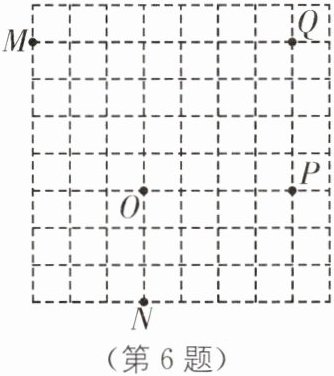
A.1个
B.2个
C.3个
D.4个
C
).
A.1个
B.2个
C.3个
D.4个
答案:
C [解析]
∵每一个小方格的边长为1km,
∴PO=4km<5km,
∴点O能被雷达监测到;
∵PN=$\sqrt{3^{2}+4^{2}}$=5(km),
∴点N能被雷达监测到;
∵PQ=4km<5km,
∴点Q能被雷达监测到;
∵PM=$\sqrt{4^{2}+7^{2}}$=$\sqrt{65}$(km),$\sqrt{65}$km>5km,
∴点M不能被雷达监测到.
综上所述,O,N,Q能被雷达监测到.故选C.
∵每一个小方格的边长为1km,
∴PO=4km<5km,
∴点O能被雷达监测到;
∵PN=$\sqrt{3^{2}+4^{2}}$=5(km),
∴点N能被雷达监测到;
∵PQ=4km<5km,
∴点Q能被雷达监测到;
∵PM=$\sqrt{4^{2}+7^{2}}$=$\sqrt{65}$(km),$\sqrt{65}$km>5km,
∴点M不能被雷达监测到.
综上所述,O,N,Q能被雷达监测到.故选C.
7.(2025·宁波慈溪期末)如图,在$\triangle ABC$中,$AB= AC= 10\ \text{cm}$,$BC= 12\ \text{cm}$,$AD\perp BC$于点D,点P为AD上的点,$DP= 2\ \text{cm}$,以P为圆心,6 cm为半径画圆,下列说法错误的是( ).
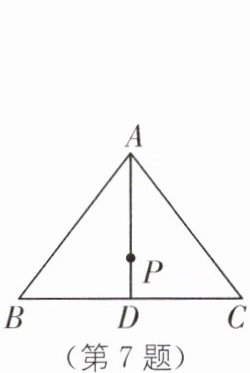
A.点A在$\odot P$上
B.点B在$\odot P$外
C.点C在$\odot P$上
D.点D在$\odot P$内

A.点A在$\odot P$上
B.点B在$\odot P$外
C.点C在$\odot P$上
D.点D在$\odot P$内
答案:
C [解析]如图,连结PB,PC.

∵AB=AC=10cm,BC=12cm,AD⊥BC于点D,
∴BD=CD=6cm,
∴AD=$\sqrt{AB^{2}-BD^{2}}$=8cm,
∴PA=AD-DP=8-2=6(cm).
在Rt△PBD中,BD=6cm,PD=2cm,
∴PB=$\sqrt{BD^{2}+PD^{2}}$=2$\sqrt{10}$cm.
∵PB=PC=2$\sqrt{10}$cm>6cm,PD=2cm<6cm,AP=6cm,
∴点A在⊙P上,点B,C在⊙P外,点D在⊙P内.故选C.
C [解析]如图,连结PB,PC.

∵AB=AC=10cm,BC=12cm,AD⊥BC于点D,
∴BD=CD=6cm,
∴AD=$\sqrt{AB^{2}-BD^{2}}$=8cm,
∴PA=AD-DP=8-2=6(cm).
在Rt△PBD中,BD=6cm,PD=2cm,
∴PB=$\sqrt{BD^{2}+PD^{2}}$=2$\sqrt{10}$cm.
∵PB=PC=2$\sqrt{10}$cm>6cm,PD=2cm<6cm,AP=6cm,
∴点A在⊙P上,点B,C在⊙P外,点D在⊙P内.故选C.
8.(安徽合肥自主招生)在矩形ABCD中,$AB= 8$,$BC= 3\sqrt{5}$,点P在边AB上,且$BP= 3AP$,如果圆P是以点P为圆心,PD为半径的圆,那么下列判断正确的是(
A.点B,C均在圆P外
B.点B在圆P外、点C在圆P内
C.点B在
D.点B,C均在圆P内
C
).A.点B,C均在圆P外
B.点B在圆P外、点C在圆P内
C.点B在
圆
P内、点C在圆P外D.点B,C均在圆P内
答案:
C [解析]
∵AB=8,点P在边AB上,且BP=3AP,
∴AP=2,BP=6,
∴PD=$\sqrt{(3\sqrt{5})^{2}+2^{2}}$=7,PC=$\sqrt{PB^{2}+BC^{2}}$=$\sqrt{6^{2}+(3\sqrt{5})^{2}}$=9.
∵PB=6<7,PC=9>7,
∴点B在圆P内、点C在圆P外.故选C.
∵AB=8,点P在边AB上,且BP=3AP,
∴AP=2,BP=6,
∴PD=$\sqrt{(3\sqrt{5})^{2}+2^{2}}$=7,PC=$\sqrt{PB^{2}+BC^{2}}$=$\sqrt{6^{2}+(3\sqrt{5})^{2}}$=9.
∵PB=6<7,PC=9>7,
∴点B在圆P内、点C在圆P外.故选C.
查看更多完整答案,请扫码查看


