《2025年实验班提优训练九年级数学上册浙教版》

1.(2024·杭州拱墅区文澜中学期末)二次函数$y= ax^{2}+bx+c$的部分图象如图所示,则方程$a(x+3)^{2}+b(x+3)+c= 2$的根是______.

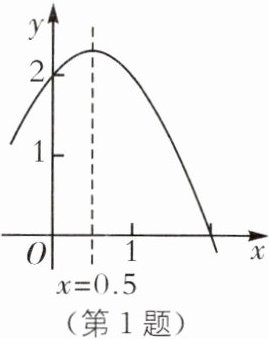
x=-3或-2

答案： x=-3或-2 [解析]由二次函数y=ax²+bx+c的图象可知,图象过(0,2),(1,2),所以方程ax²+bx+c=2的根是x=0或1,所以方程a(x+3)²+b(x+3)+c=2的根满足x+3=0或1,解得x=-3或-2.所以方程a(x+3)²+b(x+3)+c=2的根是x=-3或-2.

2. 中考新考法 解题方法型阅读理解题 (2024·云南曲靖期末)在学习二次函数与一元二次方程时,从二次函数$y= ax^{2}+bx+c$的图象可得如下结论.
如果抛物线$y= ax^{2}+bx+c$与x轴有公共点,公共点的横坐标是$x_{0}$,那么当$x= x_{0}$时,函数值是0,因此$x= x_{0}是方程ax^{2}+bx+c= 0$的一个根.
同学们,请你结合所学的数学知识解决下列问题.
已知二次函数$y= x^{2}+(m-3)x+1-2m$(m为常数).
(1)若二次函数与x轴两交点的横坐标为$x_{1},x_{2}$,且$x_{1}+x_{2}= 4$,求二次函数的表达式；
(2)不论m为何值,该函数的图象都会经过一个定点,求定点的坐标；
(3)在(1)的条件下,当$x= n,q$时,对应的函数值为N,Q,若$|n-q|= 3$,求证：$2(N+Q)\geqslant 5$.

答案：
(1)由题意,得x₁+x₂=3-m,
∴3-m=4,
∴m=-1,
∴二次函数的表达式为y=x²-4x+3.
(2)由题意,得y=x²+(m-3)x+1-2m=m(x-2)+x²-3x+1.
∵不论m为何值,该函数的图象都会经过一个定点,
∴x-2=0,即x=2,此时y=-1.
∴定点的坐标为(2,-1).
(3)由
(1),得抛物线为y=x²-4x+3.
∵|n-q|=3,
∴n-q=±3.①n-q=3时,n=q+3,
∴N+Q=(3+q)²-4(3+q)+3+q²-4q+3=9+6q+q²-12-4q+3+q²-4q+3=2q²-2q+3=2(q-$\frac{1}{2}$)²+$\frac{5}{2}$.
∴当q=$\frac{1}{2}$时,N+Q取最小值为$\frac{5}{2}$,
∴N+Q≥$\frac{5}{2}$,
∴2(N+Q)≥5;②当n-q=-3时,n=q-3.
∴N+Q=(q-3)²-4(q-3)+3+q²-4q+3=2(q-$\frac{7}{2}$)²+$\frac{5}{2}$,
∴当q=$\frac{7}{2}$时,N+Q取最小值为$\frac{5}{2}$,
∴N+Q≥$\frac{5}{2}$,
∴2(N+Q)≥5.综上所述,2(N+Q)≥5.

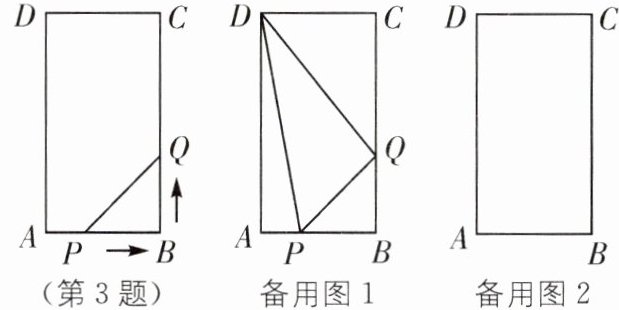
3. 如图,在矩形ABCD中,$AB= 6\ \text{cm}$,$BC= 12\ \text{cm}$,点P从点A出发,沿AB边向点B以1 cm/s的速度移动,同时,点Q从点B出发沿BC边向点C以2 cm/s的速度移动. 如果P,Q两点在分别到达B,C两点后就停止移动,回答下列问题：
(1)运动开始后第几秒时,$\triangle PBQ的面积等于8\ \text{cm}^{2}$？
(2)计算四边形DPBQ的面积,并探索一个与计算结果有关的结论.
(3)设运动开始后第$t(0\lt t\lt6)$秒时,五边形APQCD的面积为$S\ \text{cm}^{2}$,写出S与t的函数关系式,并求出S的最小值.

答案：
(1)设经过t秒,△PBQ的面积等于8cm²,则BP=(6-t)cm,BQ=2t cm,
∴S△PBQ=$\frac{1}{2}$×(6-t)×2t=8,即t²-6t+8=0,解得t=2或4.即经过2秒或4秒,△PBQ的面积等于8cm².
(2)S四边形DPBQ=6×12-$\frac{1}{2}$t×12-$\frac{1}{2}$×6(12-2t)=72-36=36,
∴四边形DPBQ的面积是固定值36.结论:四边形DPBQ的面积是定值36.
(3)根据
(1)中所求出的S△PBQ=$\frac{1}{2}$PB·BQ=$\frac{1}{2}$×(6-t)×2t,整理,得S△PBQ=-t²+6t(0＜t＜6).则S=S矩形ABCD-S△PBQ=72-(-t²+6t)=t²-6t+72=(t-3)²+63(0＜t＜6),当t=3时,S有最小值,最小值为63,故当t=3时,五边形APQCD的面积最小,最小值是63cm².

4.(2024·金华义乌绣湖中学期末)某商店销售一种销售成本为40元/千克的水产品,若按50元/千克销售,一个月可售出500千克,销售单价每涨价1元,月销售量就减少10千克.
(1)写出月销售量y(单位：千克)与售价x(单位：元/千克)之间的函数关系式.
(2)在月销售成本不超过10000元的情况下,当售价x定为多少时可获得最大月利润？并求出最大月利润.

答案：
(1)由题意,得月销售量y=500-10(x-50)=1000-10x,
∴y与x之间的函数表达式为y=-10x+1000.
(2)设月销售利润为w元.由题意,得w=y(x-40)=(-10x+1000)(x-40)=-10x²+1400x-40000=-10(x-70)²+9000.又月销售成本不超过10000元,
∴40[500-(x-50)×10]≤10000,解得x≥75.
∵-10＜0,
∴当x≥75时,w随x的增大而减小.
∴当x=75时,w有最大值,最大值为8750.
∴当售价定为75元/千克时,会获得最大月利润,最大月利润是8750元.