《2025年星推荐涂教材高中数学选择性必修第三册人教版》

1. (2025·山东日照检测)甲、乙、丙三个人踢毽子，互相传递，每人每次只能踢一下，由甲开始踢，经过 4 次传递后，毽子又被踢回给甲，则不同的传递方式共有(B)

A.4 种
B.6 种
C.10 种
D.16 种

答案：
1.B解析:分两类:甲第一次踢给乙时，满足条件的有3种传递方式(如图).　　　　　　　 　同理，甲先传给丙时，满足条件的也有3种传递方式.　由分类加法计数原理可知，共有3 + 3 = 6(种)传递方式.

2. (2025·湖南长沙模拟)集合 $ P = \{ x,1 \} $，$ Q = \{ y,1,2 \} $，其中 $ x,y \in \{ 1,2,3,·s,9 \} $，且 $ P \subseteq Q $。把满足上述条件的一对有序整数对 $ (x,y) $ 作为一个点的坐标，则这样的点的个数是(B)

A.9
B.14
C.15
D.21

答案： 2.B解析:当x = 2时，x≠y，点的个数为1×7 = 7.当x≠2时，
∵P⊆Q，
∴x = y.
∴x可从3,4,5,6,7,8,9中取，有7种方法.因此满足条件的点共有7 + 7 = 14(个).

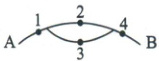
3. (2025·江苏徐州模拟)如图所示，在 A，B 间有四个焊接点 1，2，3，4，若焊接点脱落导致断路，则电路不通，那么 A，B 之间电路不通时焊接点脱落的不同情况有(C)


A.9 种
B.11 种
C.13 种
D.15 种

答案： 3.C解析:按照可能脱落的个数分类讨论.若脱落1个，则有
(1),
(4)，共2种情况;若脱落2个，则有(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)，共6种情况;若脱落3个，则有(1,2,3),(1,2,4),(1,3,4),(2,3,4)，共4种情况;若脱落4个，则有(1,2,3,4)，共1种情况.综上，共有2 + 6 + 4 + 1 = 13(种)情况.

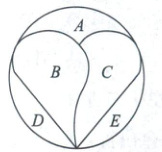
4. (2025·江苏镇江检测)如图，积木拼盘由 A，B，C，D，E 五块积木组成，若每块积木都要涂一种颜色且为了体现拼盘的特色，相邻的区域需涂不同的颜色(如：A 与 B 为相邻区域，A 与 D 为不相邻区域)，现有五种不同的颜色可供挑选，则不同的涂色方法的种数是(A)


A.960
B.240
C.480
D.720

答案： 4.A解析:先涂A，则A有5种涂法，再涂B，因为B与A相邻，所以B的颜色只要与A不同即可，有4种涂法，同理C有3种涂法，D有4种涂法，E有4种涂法.　由分步乘法计数原理，可知不同的涂色方法种数是5×4×3×4×4 = 960.

5. (多选题)(2025·江苏苏州模拟)现有不同的红球 4 个，黄球 5 个，绿球 6 个，则下列说法正确的有(ABD)

A.从中任选 1 个球，有 15 种不同的选法
B.若每种颜色选出 1 个球，则有 120 种不同的选法
C.若要选出不同颜色的 2 个球，则有 31 种不同的选法
D.若要不放回地依次选出 2 个球，则有 210 种不同的选法

答案： 5.ABD解析:从中任选1个球，有4 + 5 + 6 = 15(种)不同的选法，所以A项正确;若每种颜色选出1个球，则有4×5×6 = 120(种)不同的选法，所以B项正确;若要选出不同颜色的2个球，则有4×5 + 5×6 + 4×6 = 74(种)不同的选法，所以C项错误;若不放回地依次选出2个球，则有15×14 = 210(种)不同的选法，所以D项正确.

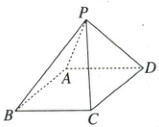
6. (2025·安徽巢湖月考)现有 5 种不同的颜色，给如图所示的几何体的五个顶点 P，A，B，C，D 涂色，要求同一条棱上的两个顶点颜色不能相同，则不同涂色方法的种数为(C)


A.240
B.360
C.420
D.480

答案： 6.C解析:第一类，顶点A,C同色，顶点P有5种颜色可供选择，顶点A有4种颜色可供选择，顶点B有3种颜色可供选择，此时顶点C与顶点A同色，只有1种颜色可选，顶点D有3种颜色可选，不同的方法共有5×4×3×1×3 = 180(种);第二类，顶点A，C不同色，顶点P有5种颜色可供选择，顶点A有4种颜色可供选择，顶点B有3种颜色可供选择，此时顶点C与顶点A不同色，有2种颜色可选，顶点D有2种颜色可选，不同的方法共有5×4×3×2×2 = 240(种).综上，不同的方法共有180 + 240 = 420(种).故选C.